다항식 시간에 해결하지 못하는 문제가 근사해도 구하기 힘들다면 해 탐색 알고리즘을 사용한다
1. 백트래킹 기법 (Backtracking)
해를 찾는 도중에 막히면 (= 해가 아니면) 되돌아가서 다시 해를 찾는 기법으로, 최적화(optimization) 문제와 결정(decision) 문제를 해결할 수 있다
* 최적화 문제: 문제의 조건을 만족하는 해의 최대값 or 최솟값 등을 구하는 문제
* 결정 문제: 문제의 조건을 만족하는 해의 존재 여부를 답하는 문제
여행자 문제 (Traveling Salesman Problem, TSP) 백트래킹 알고리즘
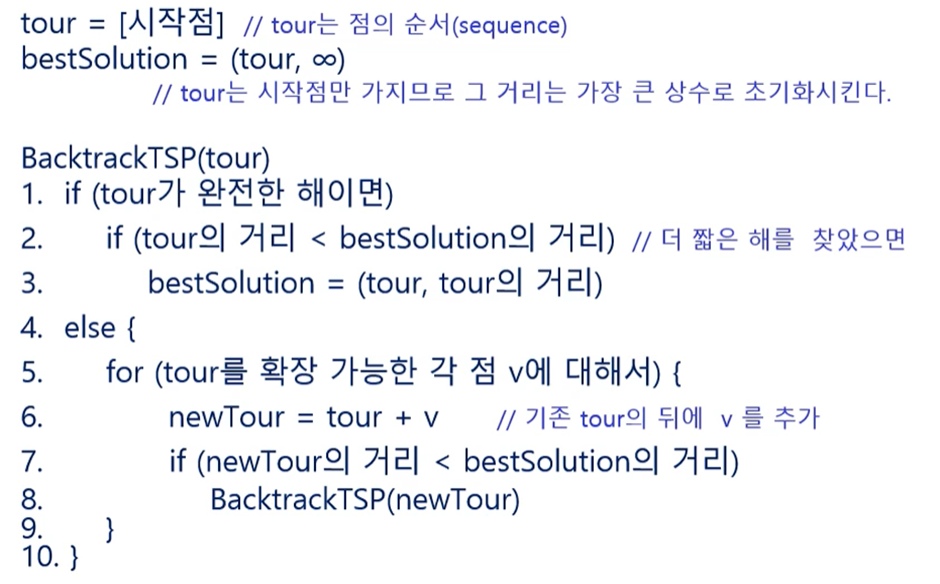



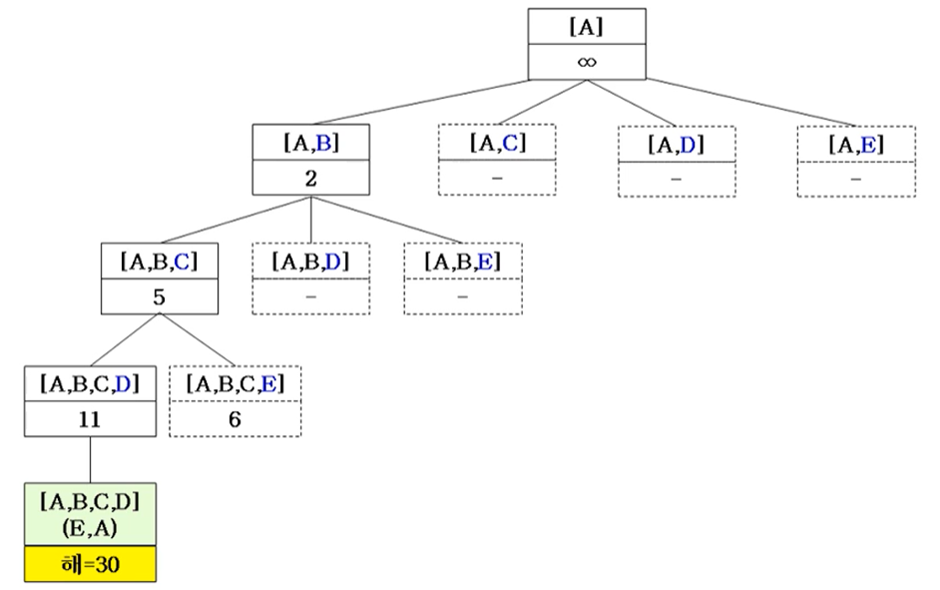




최악의 경우 2^n개의 노드를 모두 탐색해야 하는 지수 시간이 걸리며, 이는 모든 경우를 다 검사하여 해를 찾는 완결 탐색 (Exhaustive Search)의 시간복잡도와 거의 같다
* 다만 가지치기가 이루어지므로 완결 탐색보다 효율적!
트리를 끝까지 내려가는 깊이 우선 탐색 (Depth First Search, DFS)과 유사하며, 최적화 문제에 대해서는 결과적으로 대부분 노드를 탐색해야 하고 입력의 크기가 커지면 해를 찾는 것이 거의 불가능하다
2. 분기 한정 기법 (Branch-and-Bound)
- 백트래킹 기법의 단점을 보완하는 탐색 기법으로, 각 노드 (상태)에 특정한 값 (한정값)을 부여해, 이를 활용한 가지치기로 더 빠르게 해를 찾는다
- 각 상태에서 한정값을 계산하는 방법은 문제에 따라 다르며, 하나의 상태에 대한 탐색을 마친 후에는 탐색할 상태 집합 중 가장 작은 한정값을 가진 상태를 탐색한다 (= 최선 우선 탐색)
- 최적해를 찾은 후에, 탐색하여야 할 나머지 노드의 한정값이 최적해의 값과 같거나 나쁘면 더 이상 탐색하지 않으며 최적해가 있을 만한 영역을 먼저 탐색한다


여행자 문제 (Traveling Salesman Problem, TSP) 백트래킹 알고리즘
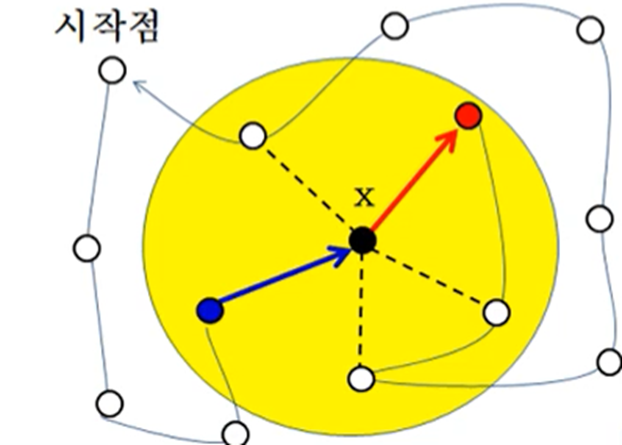
점 x의 한정값 = 시작점에서 x까지의 거리에 다른 남은 점들은 1번씩 방문하고 시작점으로 돌아오는 경로의 예측 길이 = 앞으로 방문해야 할 각 점에 연결된 선분 중 가장 짧은 두 선분의 가중치의 평균들의 합
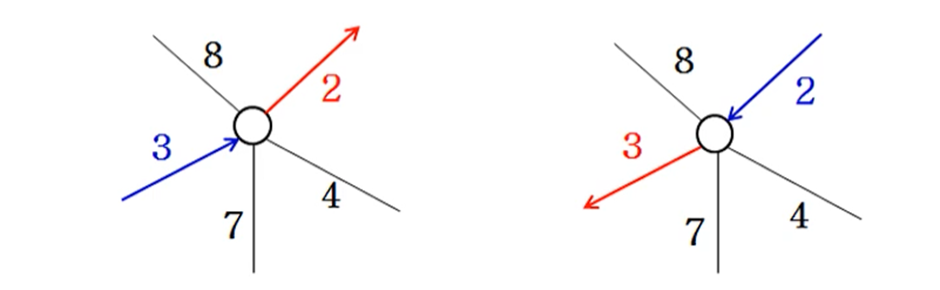



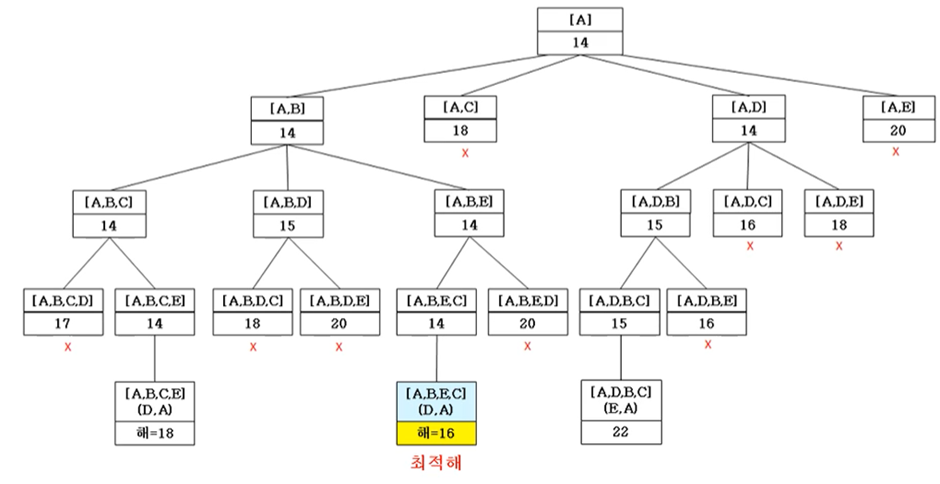
가장 우수한 한정값을 가진 노드를 먼저 탐색하는 최선 우선 탐색 (Best First Search, BFS)으로, 최적화 문제에서는 분기 한정 기법이 백트래킹 기법보다 우수한 성능을 보인다
* 위의 예제에서 백트래킹 알고리즘은 51개의 노드를 방문, 분기 한정 알고리즘은 22개를 방문
3. 유전자 알고리즘 (Genetic Algorithm, GA)
다윈의 진화론으로부터 창안된 해 탐색 알고리즘으로, ‘적자생존’ 개념을 최적화 문제에 도입했다

- 여러 개의 해를 임의로 생성해 초기 세대 G0으로 정의
- 반복문을 통해 현재 세대의 해로부터 다음 세대의 해를 생성
- 반복문이 끝났을 때, 마지막 세대에서 가장 우수한 해 반환
위 과정의 해들은 최적해 or 근접한 해가 될 수 있으므로 후보해(candidate solution)로 부른다

후보해의 평가는 후보해의 값을 계산하는 것이며 여행자 문제의 겨우 도시 간의 거리를 계산한다
= 후보해의 값 = 후보해의 적합도(fitness value) ~ 최적해의 값에 근접할수록 우수한 해
3가지 (선택/교차/돌연변이) 연산을 통해 현재 세대의 후보해에서 다음 세대의 후보해를 생성한다
a. 선택(selection) 연산
현재 세대의 후보해 중에서 우수한 후보해를 선택하는 방법으로, 룰렛 휠(roulette wheel) 방법으로 간단히 구현할 수 있다
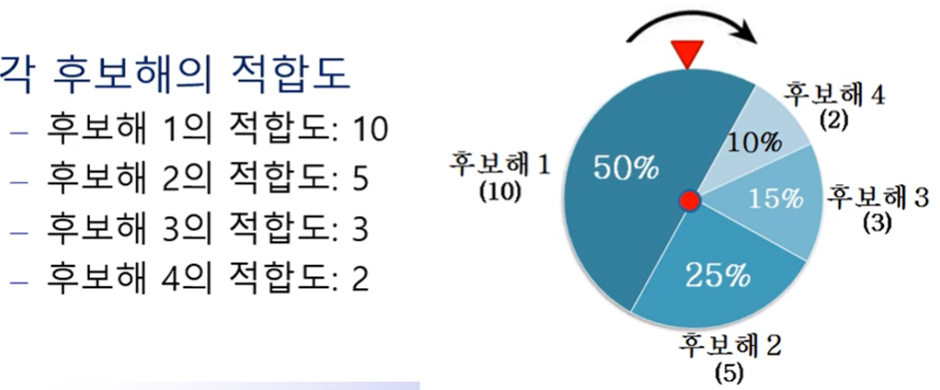
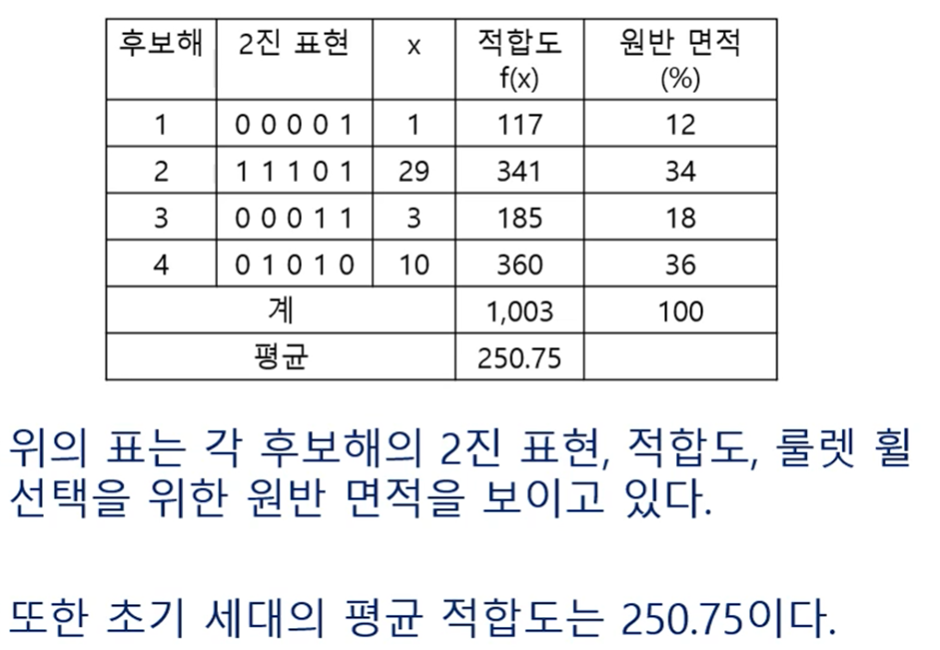
원반 면적 = (후보해의 적합도 / 모든 후보해의 적합도 합)
4개의 후보해가 있으므로, 4번 돌려서 후보해를 각각 선택한다 (중복 가능)
b. 교차(crossover) 연산
염색체가 교차하는 것을 모방한 방식으로, 선택 연산을 수행한 후에 교차해서 새로운 후보해를 생성한다
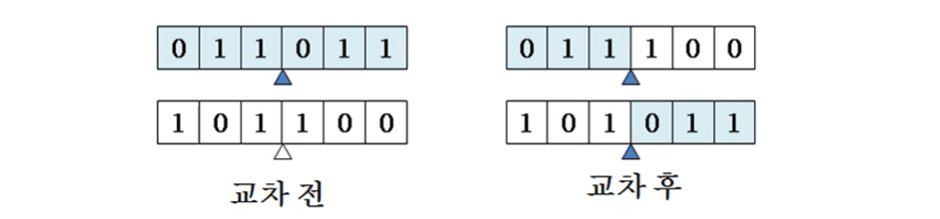
선택 연산의 후보해보다 우수한 후보해를 생성하는 것이 목적이며, 교차 연산을 수행할 후보해의 비율을 교차율(crossover rate)이라고 한다 (일반적으로 0.2 ~ 1.0 사이)
c. 돌연변이(mutation) 연산
교차 연산이 수행된 후에 아주 작은 확률로 후보해의 일부분을 임의로 변형시키는 연산이다
이 확률을 돌연변이율(mutation rate)이라고 하며, 일반적으로 (1/PopSize: 모집단 크기, 한 세대의 후보해의 수) ~ (1/Length: 후보해를 이진 표현했을 때, bit 수) 사이이다






여행자 문제 (Traveling Salesman Problem, TSP) 유전자 알고리즘
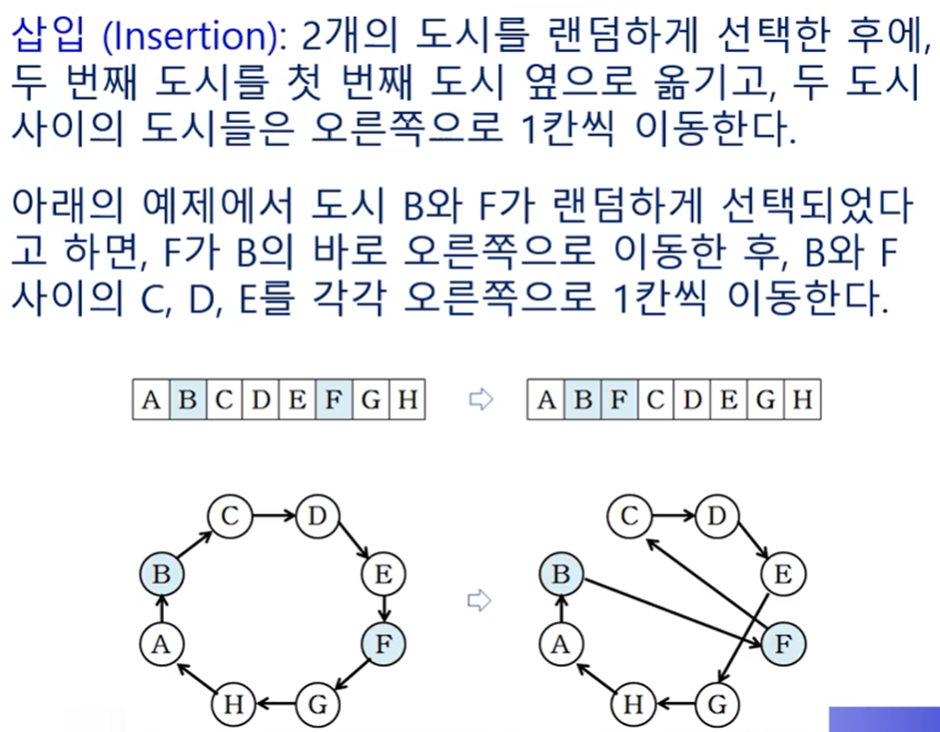
시작 도시부터 각 도시를 중복없이 나열한 후보해, 2가지 (2점, 사이클) 교차 연산을 사용한다


이처럼 유전자 알고리즘은 모집단의 크기, 교차율, 돌연변이율 등의 매개변수에 대한 다양한 실험과 조절이 필요하며, 루프의 종료 조건과 어떤 연산(선택, 교차, 돌연변이..)이 적절한지 여부도 실험을 통해 결정하는 만큼 대부분의 경우 매우 우수한 해를 찾는다

4. 모의 담금질 기법 (Simulated Annealing)
후보해에 대한 이웃해를 정의, 초기 탐색에 확률 개념을 도입하여 이웃해로 이동하며 탐색할 때 더 나쁜 해(위 방향)로 이동할 수도 있다. T가 낮아질 수록 점차 아래 방향으로 향하며 더 이상 아래로 탐색할 수 없는 지역 최적해(local optimum)에 이르렀을 때, 다시 위 방향을 탐색하다가 운 좋게 전역 최적해(global optimum)를 찾을 수도 있다
* 여러 개의 후보해를 가지는 유전자 알고리즘과 달리 하나의 초기 해로부터 탐색!






'Computer Science > Algorithm' 카테고리의 다른 글
| [HUFS/알고리즘] #8 근사 알고리즘 (0) | 2022.05.09 |
|---|---|
| [HUFS/알고리즘] #7 NP-완전 문제 (0) | 2022.05.02 |
| [HUFS/알고리즘] #6 정렬 알고리즘 (0) | 2022.04.18 |
| [HUFS/알고리즘] #5 그리디 알고리즘(2) (0) | 2022.04.11 |
| [HUFS/알고리즘] #4 그리디 알고리즘(1) (0) | 2022.04.04 |