[HUFS/알고리즘] #4 그리디 알고리즘(1)

그리디(Greedy) 알고리즘

그리디(= 탐욕) 알고리즘: 가능한 해들 중에서 가장 좋은 해를 찾는 최적화(optimization) 문제를 해결하는 알고리즘, 앞뒤 데이터 간 관계를 고려하지 않고 수행 과정에서 최소 or 최대값을 가진 데이터만 근시안적으로 선택

 

가장 작은 or 큰 값으로 부분적인 최적해를 찾아 문제의 최적해 도출

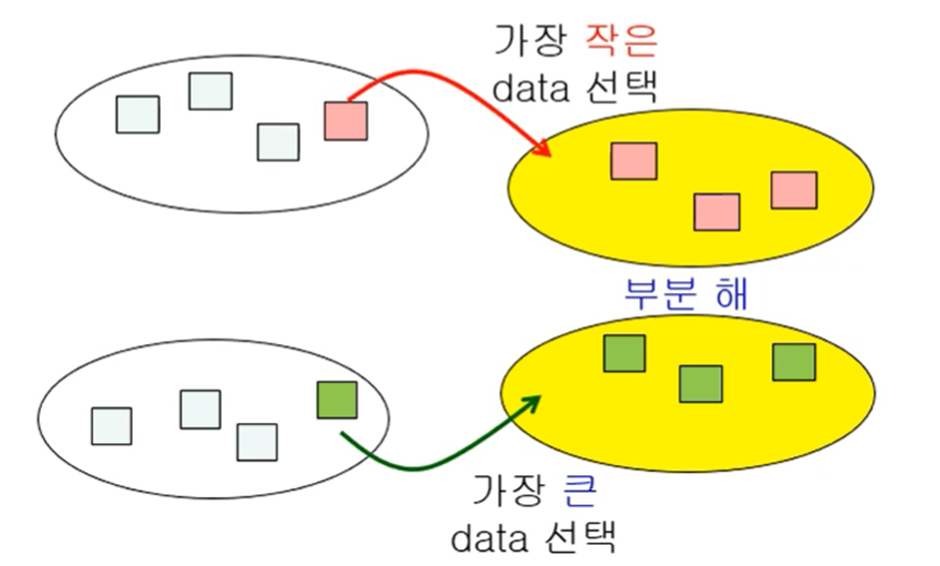
* 한 번 데이터를 선택하면 번복하지 않아서, 알고리즘이 단순하고 제한적인 문제 해결에 적합

 

1. 동전 거스름돈 문제

남은 액수를 초과하지 않는 조건 하에 가장 큰 액면의 동전을 취하는 방법? (500, 100, 50, 10, 1)

 

CoinChange 알고리즘 (무조건 큰 액면부터 근시안적으로 선택)

만약 160원 단위의 동전이 있다면, 그리디 알고리즘이 항상 최적의 답을 주지 못함

 

2. 최소 신장 트리(Minimum Spanning Tree)

주어진 가중치 그래프에서 사이클 없이 모든 점을 연결시킨 트리들 중 선분들의 가중치 합이 최소인 트리 (입력: 1개의 연결요소(connected component)로 된 가중치 그래프)

 

가중치의 합이 가장 작고(= 최소) 모든 노드를 포함(= 신장)하는 트리

그래프의 점이 n개일 때, 신장 트리는 정확히 n-1개의 선분이 있다 (n개부터는 사이클)

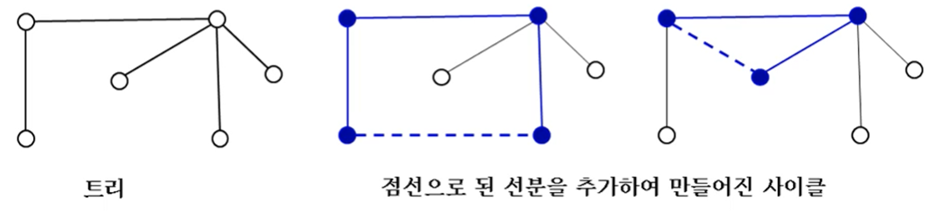
2-1. 크러스컬(Kruskal) 알고리즘: 최소 비용을 정렬해 놓고 사이클을 피해 가장 작은 순으로 선택

 

Kruskal 최소 신장 트리 알고리즘

1. 가중치의 오름차순으로 선분들을 정렬, 작은 순으로 T에 추가

2. 사이클이 만들어지는 경우 제외

3. 최종해 도출

처음 선분을 정렬할 때, O(nlogn) / T를 초기화 할 때 O(1) / 사이클 검사 상수 시간

~ O(nlogn)의 시간 복잡도 (n은 그래프에 있는 선분의 수)

 

2-2. 프림(Prim) 알고리즘: 임의의 점 하나를 선택하고 n-1개의 선분을 하나씩 추가

 

1. 점 c가 시작점일 때 c를 0으로, 인접 선분을 제외한 점을 ∞로 초기화한다

2. 최소 가중치의 점을 T에 추가하고 b와 연결된 점을 다시 선분의 가중치로 갱신한다

3. 가중치가 동일한 f 기준, e는 가중치로 초기화, d는 이미 더 작은 값이라 갱신되지 않는다

4. 최소 점을 기준으로 이동, 다시 가중치가 더 작은 값으로 갱신한다

5. 반복하며 최종해를 도출한다

T 밖의 점으로 뻗어 나가는 구조이기 때문에 사이클이 생기지 않는다

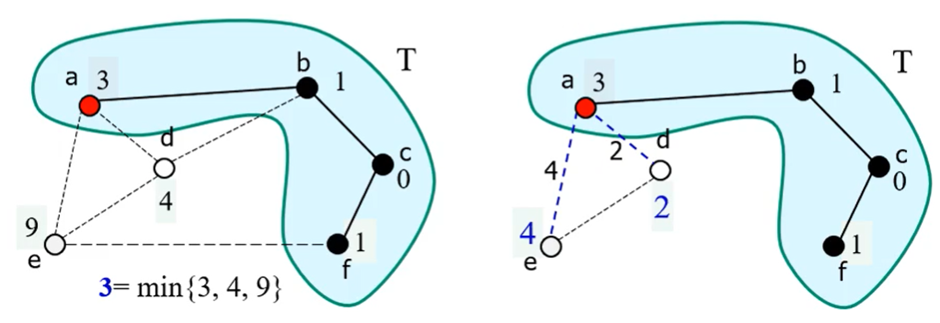
while 루프가 n-1번 반복 / 값이 최소인 점을 찾을 때 O(n)

~ (n-1) * O(n) = O(n^2)의 시간 복잡도

 

Kruskal 알고리즘은 n개의 트리들이 점차 합쳐져 1개의 신장 트리가 되는 과정,

Prim 알고리즘은 1개의 트리가 자라나 신장 트리가 되는 과정이다

* 최소 비용 선로, 파이프 네트워크(광케이블, 배수로, 송유관 ..) 등을 설치하는데 활용

 

3. 최단 경로 찾기

주어진 가중치 그래프의 한 출발점에서 또 다른 도착점까지의 최단 경로를 찾는 문제로, 가장 대표적으로 다익스트라 알고리즘이 있다

 

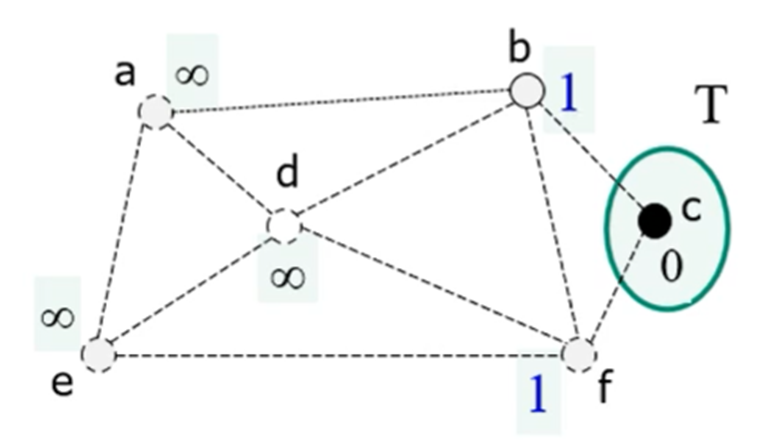
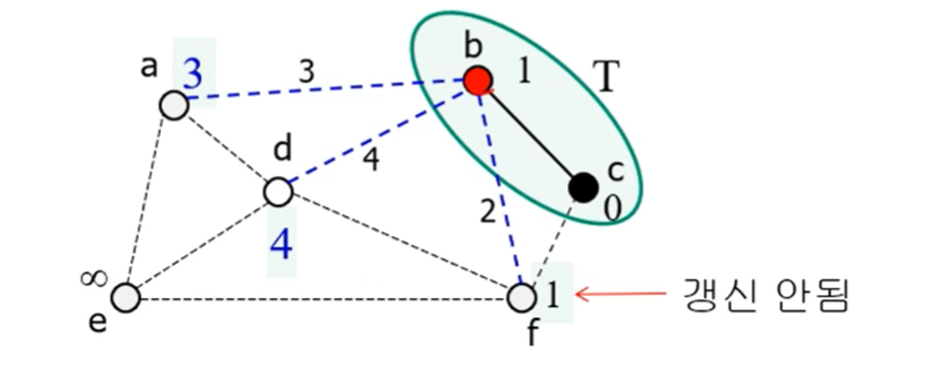
다익스트라(Dijkstra) 알고리즘: 주어진 출발점에서 시작해 최단 거리가 확정되지 않은 점들 중에서 출발점으로부터 가장 가까운 점을 추가하고 그 점의 최단 거리를 확정해 비교하는 방식

 

다익스트라 알고리즘

1. 시작점에 인접한 점의 가중치 합을 구한다

2. 더 작은 값을 기준으로 다시 인접한 점의 가중치 합을 구하고 전체를 비교한다

3. 다시 가장 작은 값을 기준으로 인접한 점의 가중치 합을 구하고 비교하는 과정을 반복한다

4. 이 과정에서 점에 더 작은 가중합이 생긴다면 값을 갱신하고 다시 비교 대상에 포함한다

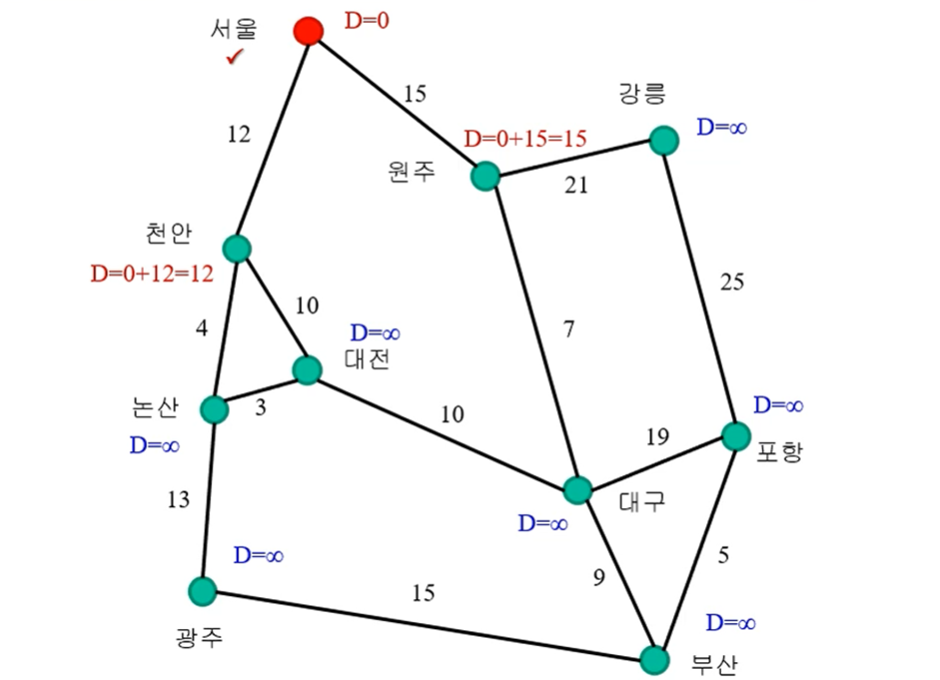
while 루프가 n-1번 / 최소 점 찾기 O(n) / 각각의 점 갱신 O(n)

~ (n-1) * {O(n) + O(n)} = O(n^2)의 시간 복잡도

* 네비게이션 및 지도 서비스, 네트워크, 로봇 공학, 교통 공학, VLSI 디자인 등에 응용

 

4. 배낭(Knapsack) 문제

n개의 물건이 있고, 각 물건은 무게와 가치가 있으며, 배낭이 한정된 무게를 담을 수 있을 때, 최대의 가치를 갖도록 배낭에 물건을 넣는 문제

• 부분 배낭(Fractional Knapsack) 문제: 물건을 부분적으로 담는 것을 허용 (그리디 알고리즘)
• 배낭 문제 (0/1 배낭 문제): 물건을 통째로 넣어야 하는 일반적인 배낭 문제 (동적 계획 알고리즘, 백트래킹 기법, 분기 한정 기법)

 

부분 배낭 문제 그리디 알고리즘

부분 배낭 문제 그리디 알고리즘 해설

단위 무게당 가치 계산 O(n) / 내림차순 정렬 O(nlogn) / while 루프 최대 n번 O(1) / 비교 O(1)

~ O(n) + O(nlogn) + n * O(1) + O(1) = O(nlogn)의 시간 복잡도

* 자원을 할당하는 조합론, 계산이론, 암호학, 응용수학 분야의 기초이며 원자재 및 투자에도 응용