[HUFS/알고리즘] #6 정렬 알고리즘

정렬(Sorting) 알고리즘

내부(Internal) 정렬

• 입력의 크기가 주기억 장치의 공간보다 작은 경우 (빠름)
• 버블 정렬, 선택 정렬, 삽입 정렬
• 합병 정렬, 퀵 정렬, 힙 정렬, 쉘 정렬
• 기수 정렬 (입력이 제한된 크기 이내의 숫자로 구성될 때)

 

외부(External) 정렬:

• 입력의 크기가 주기억 장치의 공간보다 큰 경우 (느림)
• 보조 기억 장치에 있는 입력을 나누어 주기억 장치에 읽어 들인 후, 다시 보조 기억 장치에 저장
• 다방향(p-way) 합병, 다단계(Polyphase) 합병

 

1. 버블(Bubble) 정렬

이웃하는 숫자를 비교해 작은 수를 앞(위)쪽으로 이동시키는 과정을 반복해 정렬하는 알고리즘

* 작은 수가 앞으로 올라오는 과정이 마치 거품 같아 붙은 이름이다

 

위처럼 입력을 전체적으로 1번 처리하는 것을 패스(pass)라고 한다

패스를 반복하며 가장 큰 수를 아래로 내린다

이처럼 n개의 원소가 있다면 (n-1)번의 패스가 수행된다

버블 정렬 알고리즘

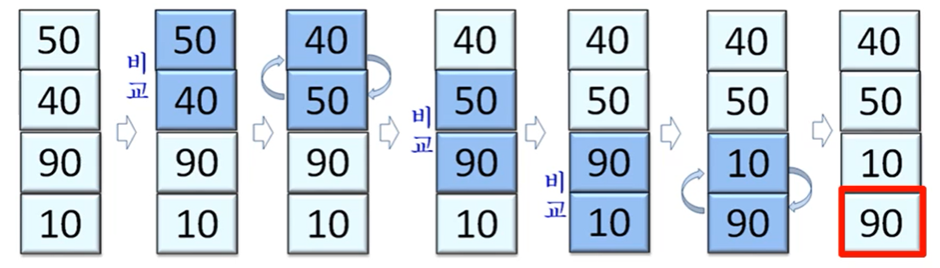
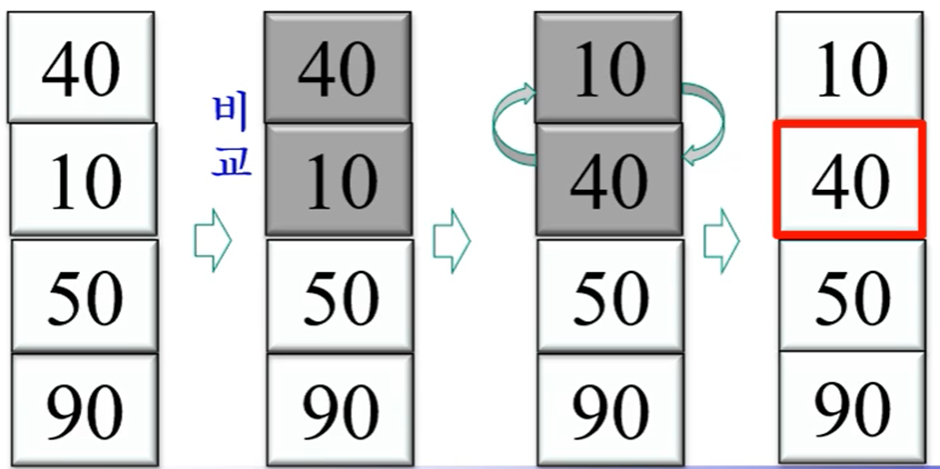
이중 for문 n(n-1)/2 / if 조건이 참일 때 자리바꿈 O(1)

~ O(n2) * O(1) = O(n2)의 시간복잡도

 

2. 선택(Selection) 정렬

배열 전체에서 최솟값을 선택에 0번 원소와 자리를 바꾸고, 다시 나머지 원소에서 최소값을 선택에 1번 원소와 자리를 바꾸는 과정을 반복해 정렬하는 알고리즘

 

마지막 2개의 원소를 비교할 때까지 반복한다

선택 정렬 알고리즘

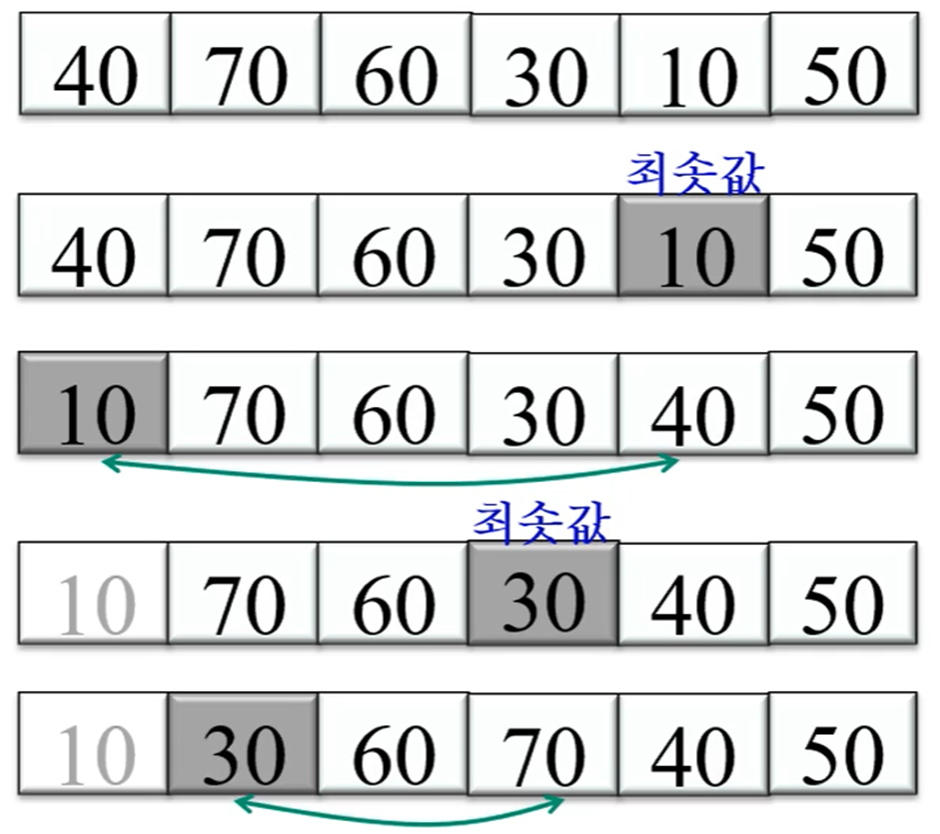
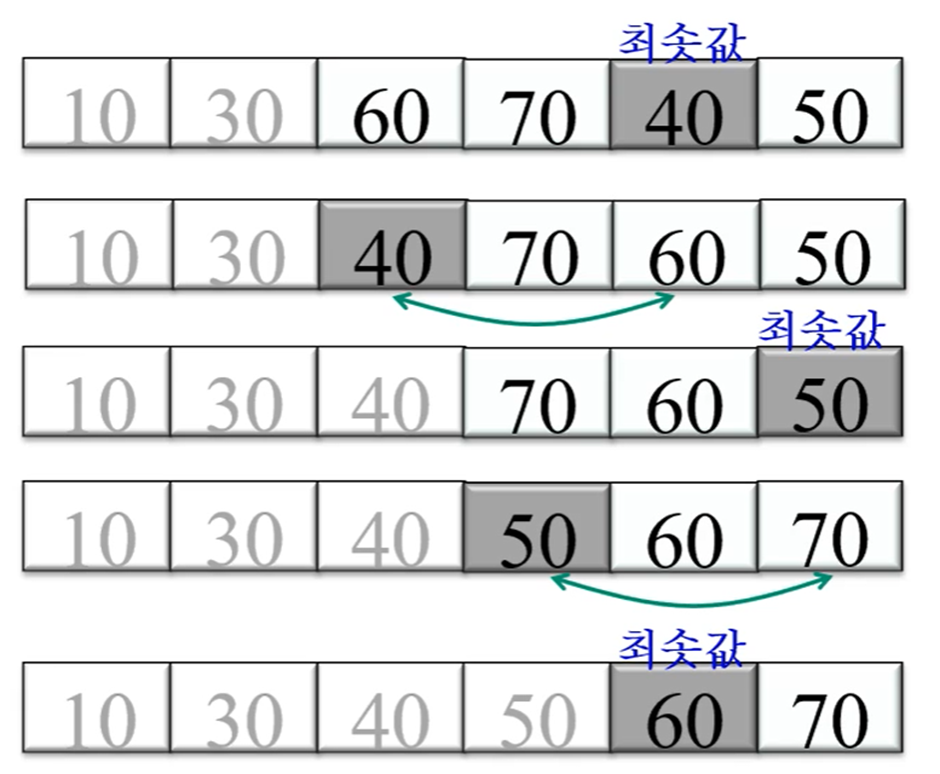
처음 for문 수행 n-1 / for문 내부의 for문 수행 n(n-1)/2 / if 조건이 참일 때 자리바꿈 O(1)

~ n(n-1)/2 * O(1) = O(n2)의 시간복잡도

 

선택 정렬은 입력이 어떤 형태여도 항상 일정한 시간복잡도를 나타낸다는 점에서 입력에 민감하지 않은(input insensitive) 알고리즘이다

 

3. 삽입(Insertion) 정렬

배열을 정렬된 (앞)부분과 정렬 안된 (뒷)부분으로 나누고 정렬 안된 부분의 가장 왼쪽 원소를 정렬된 부분의 적절한 위치에 삽입하는 과정을 반복해 정렬하는 알고리즘

* 맨 처음에는 첫 번째 원소만이 정렬된 부분이다

 

삽입 정렬 과정

삽입 정렬 알고리즘

for문 내부 while문 n(n-1)/2 / 자리 이동 O(1)

~ n(n-1)/2 * O(1) = O(n2)의 시간복잡도

 

최선의 경우: 이미 정렬되어 있다면, while 루프 조건이 항상 거짓이므로 원소의 이동도 없으며 (n-1)번 비교하고 정렬을 마친다. ~ O(n)의 시간복잡도

* 입력에 따라 수행 시간이 달라지며, 거의 정렬된 입력에 대해 다른 정렬 알고리즘보다 빠르다

 

4. 쉘(Shell) 정렬

한칸씩 비교하며 이동하는 버블 정렬이나 삽입 정렬의 단점을 보완한 방식으로, 삽입 정렬과 비슷한데, 뒷부분의 작은 숫자를 앞부분으로 빠르게 이동시키고 동시에 앞부분의 큰 숫자는 뒷부분으로 이동시킨 후 마지막에 삽입 정렬을 수행하는 알고리즘

 

1. 임의의 배열에 대해서 간격이 h가 되는 숫자끼리 h개의 그룹으로 나눈다

2. 그룹별로 삽입 정렬을 수행하고 다시 나열해준다

3. 간격을 임의로 줄여 나가며 동일한 작업을 반복하다가 마지막에는 간격을 1로 놓고 수행한다

마지막 h=1인 경우 삽입정렬과 동일한 과정이며, 최악의 경우 시간복잡도는 O(n2)

가장 좋은 성능을 보이는 간격들은 아직 연구중이며 일반적인 시간복잡도는 O(n1.5)

* 입력 크기가 매우 크지 않은 경우 성능이 좋고, 간격에 따른 그룹별 정렬 방식이 하드웨어에 적합해 임베디드(Embedded) 시스템에 주로 사용된다

 

5. 힙(Heap) 정렬

힙(Heap): 각 노드의 값이 자식 노드의 값보다 커야 하는 힙 조건을 만족하는 완전 이진트리(Complete Binary Tree)로, 이 때 노드의 값은 우선순위(priority)이며, 루트에 가장 큰 값이 저장(= 최대힙)된다.

* 값이 작을수록 우선순위가 높은 경우도 있는데, 이 경우 루트에 가장 작은 값이 저장된다

 

n개의 노드를 가진 힙으로, 높이가 log2n이며 빈 공간 없이 배열에 저장된다

이 때, 부모 노드의 인덱스는 (자식 노드의 인덱스/2)의 정수 부분이다

힙 정렬은 힙 자료 구조를 이용하는 정렬 알고리즘으로, 가장 큰 값이 루트 노드에 저장되는 최대힙(maximum heap)을 구성해 루트의 숫자를 힙의 마지막 노드와 맞바꾼 후, 힙 크기를 1개 줄여 다시 힙 조건을 만족시키고 해당 과정을 반복한다

 

힙 정렬 알고리즘

1. 루트와 마지막 노드를 맞바꿔서 힙의 노드 수가 1개 줄어든다

2. 힙 조건을 만족시키기 자식 노드 중 큰 값과 교환(DownHeap)한다

3. 힙 조건을 만족할 때까지 내려가며 자식 노드와 교환을 반복한다

4. 1~3 과정을 반복한다

5. 힙의 크기가 1이 되면 힙 정렬을 마친다

힙을 만드는 시간 O(n) / 변수 초기화 O(1) / for문 (n-1)번 / DownHeap O(logn)

~ O(n) + (n-1) * O(logn) = O(nlogn)의 시간복잡도

 

정렬 문제의 하한

버블 정렬, 선택 정렬, 삽입 정렬, 쉘 정렬, 힙 정렬, 합병 정렬, 퀵 정렬 등의 공통점은 숫자의 비교가 부분적이 아닌 숫자 대 숫자로 이루어지는 비교 정렬(Comparison Sort)이라는 점이다

* 숫자들을 한 자리씩 부분적으로 비교하는 기수 정렬과 다른 개념

 

시간복잡도의 하한(lower bound)란 특정 알고리즘의 하한이 아닌 문제가 가지는 고유의 특성 때문에 최소한으로 걸리는 시간복잡도를 의미한다.

 

1. n개의 숫자가 저장된 배열에서 최댓값을 찾는 문제의 하한(= 비교 정렬의 최소 비교 횟수)은?

~ 각 숫자를 적어도 한 번은 비교해야 하기 때문에 최소 (n-1)번의 비교가 필요!

 

2. 서로 다른 3개의 숫자의 정렬 문제의 하한은?

 

결정 트리(Decision Tree)의 노드에 따르면 이파리(단말 노드)는 3번의 비교가 필요하다

결정 트리의 높이 = 비교 정렬의 하한인데, n개를 비교할 때 n! = k개의 이파리가 있는 이진 트리의 높이는 최소 logk이며, 이는 log(n!) = O(nlogn)이므로 O(nlogn)이 비교 정렬의 하한 시간복잡도이며, 이를 점근적 하한으로 표기하면 Ω(nlogn)이다

 

6. 기수(Radix) 정렬

제한적 범위 내의 숫자들에 대해 각 자릿수 별로 부분적으로 비교해 정리하는 방법으로,

기(Radix)란 특정 진수를 나타내는 숫자를 의미! ex) 10진수: 0~9, 2진수: 0~1

어느 비교 정렬 알고리즘보다 빠르다는 장점을 가지고 있다

 

자릿수별로 정렬 예시

* 해당 자릿수가 동일하다면 전 단계 순서 기준으로 정렬! ex) 070 < 910, 131 < 035

 

정렬 알고리즘에서, 입력에 중복된 숫자가 있을 때, 정렬된 후에도 중복된 숫자의 순서가 입력에서의 순서와 동일하면 정렬 알고리즘이 안정성(Stability)을 가진다고 한다

 

중복된 입력에 대해서, 기수 정렬은 안정한 정렬

기수 정렬 알고리즘

for 루프 k번 반복 / i자리 수를 읽으며 r개로 분류 + 숫자 이동 O(n+r)

~ O(k(n+r)) = O(n)의 시간복잡도

 

기수 정렬을 1의 자리부터 k 자리로 진행하는 경우 LSD(Least Significant Digit) 기수 정렬 or RL(Right-to-Left) 기수 정렬,

반대로 k 자리부터 1의 자리로 진행하는 경우 MSD(Most Significant Digit) 기수 정렬 or LR(Left-to-Right) 기수 정렬

* 계좌 번호, 날짜, 주민등록번호 등 대용량 상용 데이터베이스 정렬 및 랜덤 128비트 초대형 파일의 정렬에 응용

* 다수의 프로세서들이 사용하는 병렬(Parallel) 환경에서 정렬 알고리즘의 기본 아이디어로 활용

 

7. 외부(External) 정렬

외부 정렬: 입력이 주기억 장치(내부 메모리)에 있는 상태에서 정렬이 수행되는 지금까지의 내부 정렬과 달리, 입력 크기가 매우 커서 보조 기억 장치에 입력을 저장할 수 밖에 없는 상태에서 수행되는 정렬

 

내부 정렬에 수용될 만큼 (1GB) 분할해 정렬하고 다른 보조 기억 장치에 부분적인 결과를 저장한다

부분 결과들을 일부씩 다시 주기억 장치로 읽어 들여서 합병(merge)을 수행

1GB 블록 2개가 2GB 블록 1개로 합병되는 과정

해당 과정을 반복하는 과정을 용량을 늘리며 반복

외부 정렬 반복

128GB의 입력과 1GB의 주기억 장치에 대한 외부 정렬 과정

전체 데이터를 몇 번 처리하는가(= pass)로 시간복잡도를 측정 = while 루프의 수행 횟수

입력 크기가 N, 메모리 크기가 M일 때, 블록 크기는 반복문 실행마다 2^k*M으로 증가

마지막 1개의 블록 크기가 2^k*M일 때 이는 N과 동일하고 while루프 수행 횟수는 k

~ 2^k = N/M, k = log2(N/M) = O(log(N/M))의 시간복잡도

 

* 물품/재고  DB, 인사 DB의 갱신, 통신/전화 회사의 전화번호 정렬, 인터넷 IP 주소 관리, 은행의 계좌 관리 등에 응용