[HUFS/알고리즘] #7 NP-완전 문제

P(polynomial) 문제 집합은 다항식 시간 복잡도를 가진 알고리즘으로 해결되는 문제들을 의미하며, O(logn), O(n), O(nlogn), O(n^2), O(n^3) 등 점근적 표기법으로 O(n^k)에 포함되는 시간 복잡도 내에서 해결된다

 

다항식보다 큰 시간복잡도를 가진 알고리즘으로 해결되는 문제 집합 들이 있는데, 이는 여러 가지 문제 집합으로 다시 분류되며, 이 중 지수 시간 시간복잡도를 가진 알고리즘으로 해결되는 문제들을 NP-완전 문제 집합이라고 한다

* 하나의 NP-완전 문제에 대해서 다항식 시간의 알고리즘을 찾아내면, 모든 다른 NP-완전 문제도 다항식 시간에 해를 구할 수 있다

 

NP 문제 집합은 이러한 P 문제 집합과 NP-완전 문제 집합을 포함하는 개념으로, 비결정적 다항식 시간 알고리즘(Nondeterministic Polynomial time)을 가진 문제들이다

= 주어진 입력에 대한 하나의 해를 추측 -> 다항식 시간이 확인되면 정답으로 판단

* 시간이 오래 걸려도 해가 구해지는 결정적 알고리즘과 달리 해를 구할 수 있을지 비결정적!

 

NP 알고리즘은 해를 찾는 알고리즘이 아닌, 해를 다항식 시간에 확인하는 알고리즘

* P 문제 또한 다항식 해를 확인하는 과정에 포함될 수 있기 때문에 NP 알고리즘에 포함

 

NP-완전 문제에 상수 조건을 달아 결정 문제로 변형 가능

문제의 변환(or 환원 = reduction)이란 문제 A를 해결하기 위해 문제 B를 해결하는 알고리즘을 이용하는 것을 의미한다

 

입력 변환과 출력 변환으로 문제 A에 문제 B의 알고리즘을 활용

예를 들어, 집합 S의 부분 집합의 합이 105(= K)인 경우를 찾는 문제 A

집합 S의 부분 집합 원소들의 합이 같은 2개의 부분 집합을 찾는 문제 B

입력을 B로 변환하며 추가된 40(=t)를 B의 해를 A의 해로 변환하며 제거

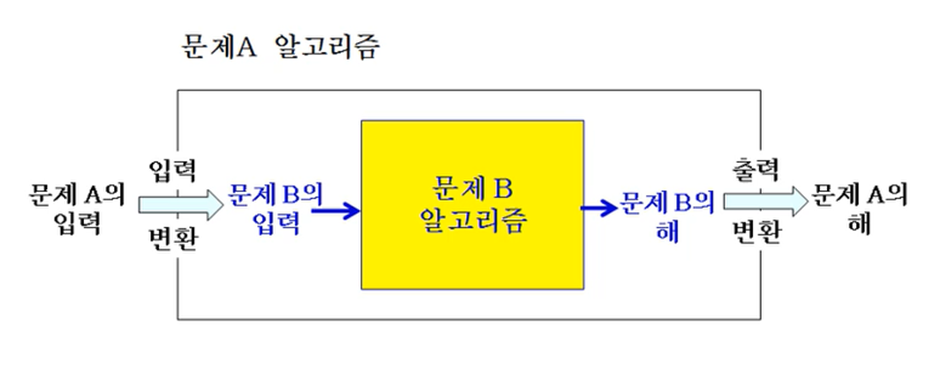
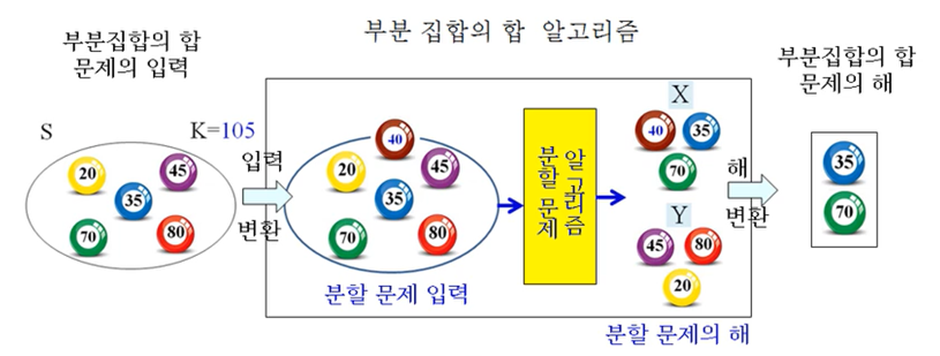
문제를 변환하는 과정의 시간복잡도는 다음 3단계의 시간복잡도의 합

1. 문제 A의 입력을 문제 B의 입력으로 변환
2. 문제 B를 위한 알고리즘이 수행되는 시간
3. 문제 B의 해를 문제 A의 해로 변환하는 시간

 

1, 3 단계는 다항식 시간 ~ 2단계 (문제 B의 시간복잡도)에 따라 전체 시간복잡도가 결정

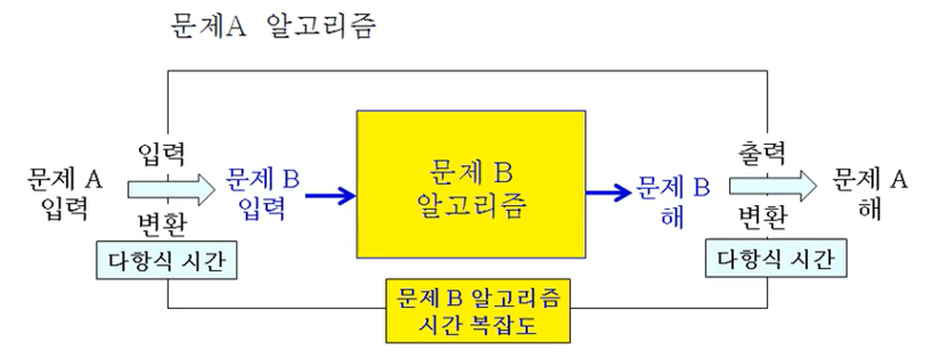
만약 2단계도 다항식 시간이 성립하면, 문제 A가 문제 B로 다항식 시간에 변환 가능(polynomial time reduction)하다고 한다

* 추가로 B가 C로 변환 가능하다면 A도 C로 변환 가능한데, NP-완전 문제들은 이러한 추이(transitive) 관계로 묶여 있어서 한 문제만 다항식 시간이 해결되면 모든 다른 NP-완전 문제들도 다항식 시간에 해결된다!

 

NP-하드(hard) 문제 집합이란 어느 문제 A에 대해서 모든 NP 문제가 문제 A로 다항식 시간에 변환이 가능한 경우의 집합으로, 문제 A가 반드시 NP 문제일 필요는 없다

 

문제 집합들 사이의 관계

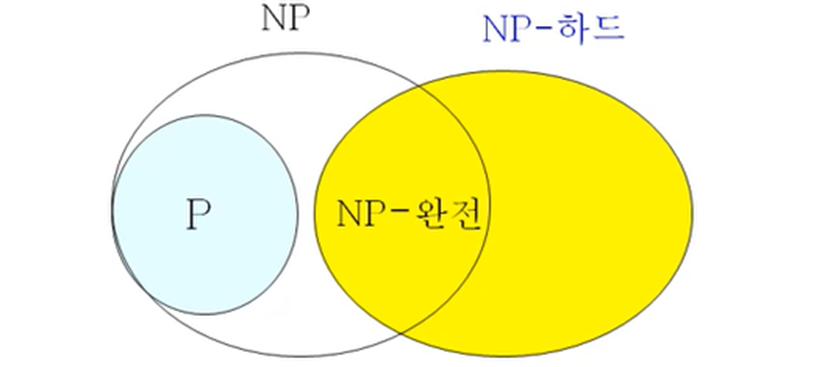
즉, 문제 A가 NP-완전 문제가 되려면..

• 문제 A는 NP 문제이고, 동시에
• 문제 A는 NP-하드 문제이다

 

NP-완전 문제

다항식 시간에 하나의 문제에서 다른 문제로 변환이 가능하며, 컴퓨터 분야 뿐만 아니라 과학, 공학, 의학, 약학, 경영학, 정치학, 금융, 문화 문야 등에 실제로 제기되는 문제들을 다룬다

1. SAT (Satisfiability)

부울 변수(Boolean variable)들이 V(OR)로 표현된 논리식이 여러 개 주어질 때 모두 만족시키는 각 부울 변수의 값을 찾는 문제

 

SAT 예시

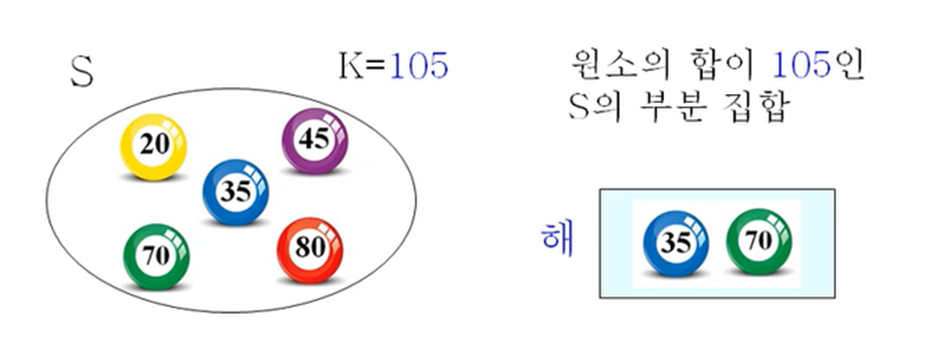
2. 부분 집합의 합 (Subset Sum)

주어진 정수의 집합 S의 원소의 합이 K가 되는 S의 부분 집합을 찾는 문제

 

부분 집합의 합 예시

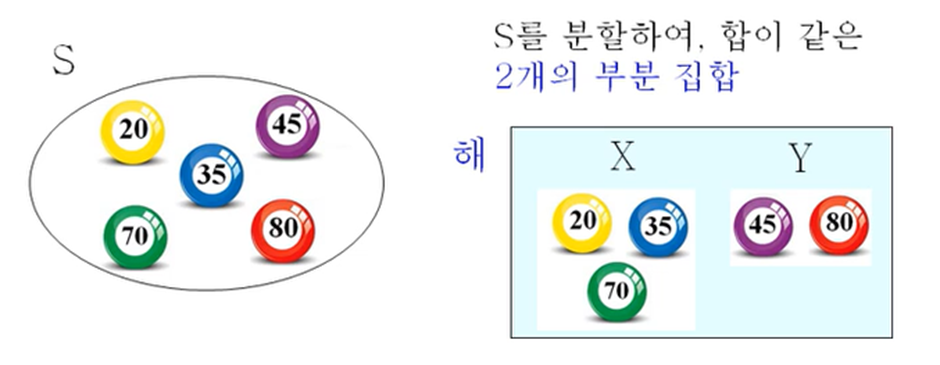
3. 분할 (Partition)

주어진 정수의 집합 S를 분할하여 원소의 합이 같은 2개의 부분 집합을 찾는 문제

 

분할 예시

4. 0-1 배낭 (Knapsack)

배낭의 용량이 C이고, n개의 물건의 각각의 무게와 가치가 주어질 때, 배낭에 담을 수 있는 최대 가치를 찾는 문제

 

0-1 배낭 예시

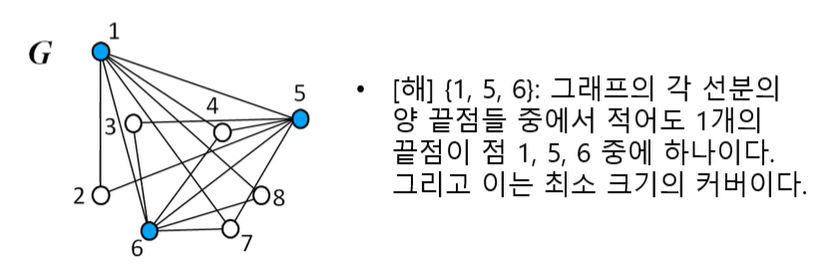
5. 정점 커버 (Vertex Cover)

주어진 그래프 G=(V,E)에서 각 선분의 양 끝점들 중 적어도 1개의 점을 포함하는 정점 커버 중 최소 크기의 정점 커버를 찾는 문제

 

정점 커버 예시

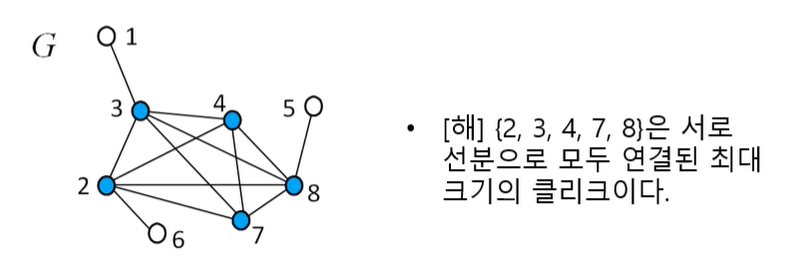
6. 클리크 (Clique)

주어진 그래프 G=(V,E)에서 모든 점들 사이를 연결하는 선분이 있는 부분 그래프인 클리크 중 최대 크기의 클리크를 찾는 문제

 

클리크 예시

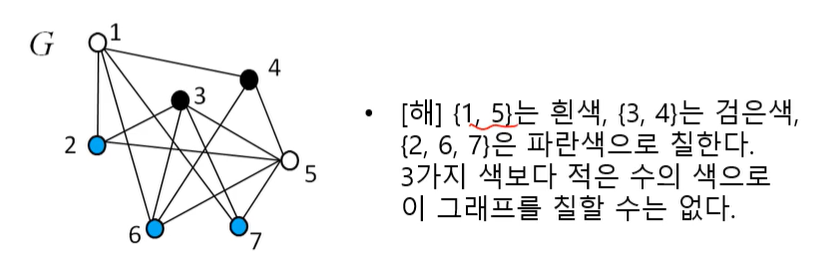
7. 그래프 색칠하기 (Graph Coloring)

주어진 그래프 G=(V,E)에서 인접한 점들을 서로 다른 색으로 색칠할 때, 가장 적은 수의 색을 사용하는 문제

 

그래프 색칠하기 예시

8. 집합 커버 (Set Cover)

주어진 집합 S에 대해서 S의 부분 집합들이 주어질 때, 부분 집합들 중에서 합집합하여 S와 같게 되는 부분 집합들인 집합 커버 중 가장 적은 수의 부분 집합으로 이루어진 집합 커버를 찾는 문제

 

집합 커버 문제

9. 최장 경로 (Longest Path)

주어진 가중치 그래프 G=(V,E)에서 시작점 s에서 도착점 t까지의 가장 긴 경로를 찾는 문제

 

최장 경로 예시

10. 여행자 문제 (Traveling Salesman)

주어진 가중치 그래프 G=(V,E)에서 한 점에서 출발해 다른 모든 점들을 1번씩만 방문하고 다시 시작점으로 돌아오는 경로 중 최단 경로를 찾는 문제

 

여행자 문제 예시

11. 헤밀토니안 사이클 (Hamiltonian Cycle)

주어진 그래프 G=(V,E)에서 한 점에서 출발해 다른 모든 점들을 1번씩만 방문하고 다시 시작점으로 돌아오는 경로 중 최단 경로를 찾는 문제 (선분의 가중치가 모두 동일한 여행자 문제와 같다)

 

헤밀토니안 사이클 예시

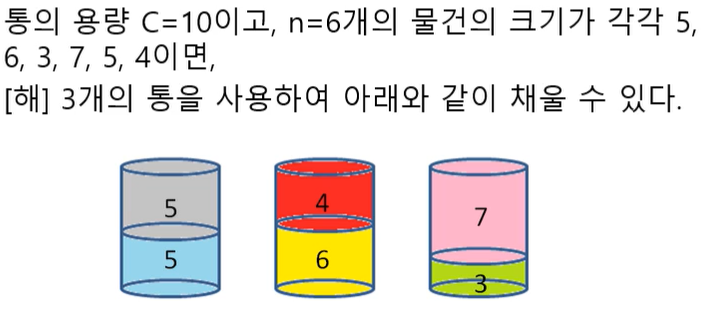
12. 통 채우기 (Bin Packing)

n개의 물건이 주어지고, 통의 용량이 C일 때, 가장 적은 수의 통을 사용하여 모든 물건을 통해 채우는 문제

 

통 채우기 예시

13. 작업 스케줄링 (Job Scheduling)

n개의 작업, 각 작업의 수행 시간, 그리고 m개의 동일한 성능의 기계가 주어질 때, 모든 작업이 가장 빨리 종료되도록 작업을 기계에 배정하는 문제

 

작업 스케줄링 예시

이 외에도 다양한 NP-완전 문제가 있으며 다항식 시간에 하나의 문제에서 다른 문제로 변환이 가능하다

 

NP-완전 문제의 변환 예시

NP-완전 문제들의 활용

SAT 활용 예시

부분 집합의 합 활용 예시

분할 활용 예시

0-1 배낭 활용 예시

정점 커버 활용 예시

집합 커버 활용 예시

독립 집합 활용 예시

클리크 활용 예시

그래프 색칠하기 활용 예시

최장 경로 / 여행자 / 헤밀토니안 사이클 활용 예시

통 채우기 활용 예시

작업 스케줄링 활용 예시