[HUFS/알고리즘] #3 분할 정복 알고리즘(2)

선택(Selection) 문제

선택 문제: n개의 숫자들 중에서 k번째로 작은 숫자를 찾는 문제

 

간단한 방법

• 최소 숫자를 찾고 제거하는 과정을 k번 반복하고 최소 숫자를 찾는다 ~ 최악의 경우 O(kn)
• 숫자들을 정렬하고 k번째 숫자를 찾는다 ~ 최악의 경우 O(nlogn)

 

선택 문제 알고리즘

 

퀵정렬과 비슷하게 선정된 피봇을 기준으로 분할하고 교환

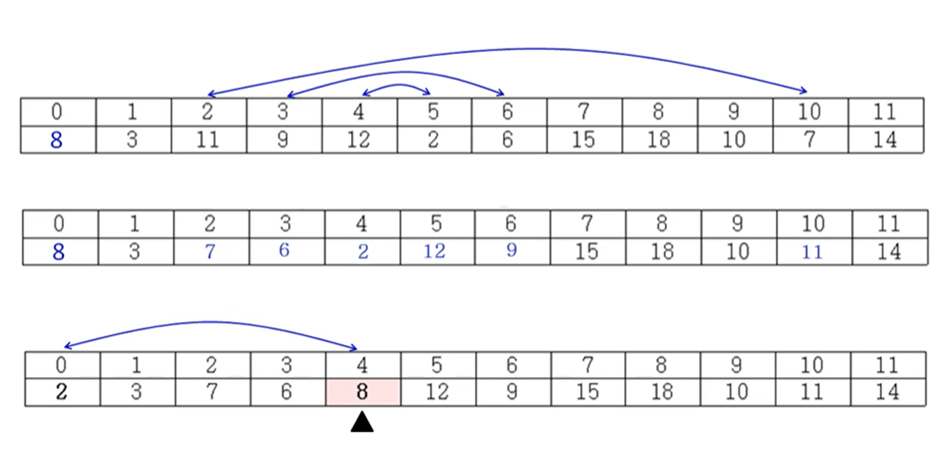
* 각 그룹의 크기를 알면, k번째 작은 숫자가 어느 그룹에 있는지 알 수 있고, 그 그룹에서 몇 번째 작은 숫자를 찾아야 하는지 알 수 있다!

 

1. Small group에 k번째 작은 숫자가 속한 경우: k번째 작은 숫자를 해당 그룹에서 찾는다
2. Large group에 k번째 작은 숫자가 속한 경우: (k – Small group의 숫자 개수 – 1) 번째로 작은 숫자를 해당 그룹에서 찾는다

선택 문제 알고리즘

선택 문제 알고리즘 해설

선택 문제 알고리즘 과정

 

1. 피봇을 A[6](=8)으로 선정하고 7번째 작은 수(k=7)를 찾는 경우 ~ Selection(A, 0, 11, 7)

2. 피봇이 A[0]으로 오도록 값을 교환

3. 피봇을 기준으로 값을 맞바꾸고 피봇보다 작고 가장 우측에 값과 피봇을 교환

4. 크기를 계산하고 조건에 일치할 때까지 값이 존재하는 그룹에 재귀호출

5. 조건에 일치하는 경우 값을 반환

선택 문제 알고리즘 고려사항

1. 피봇을 랜덤하게 정하기 때문에 분할 정복 알고리즘인 동시에 랜덤 알고리즘이다
2. 피봇이 너무 작거나 큰 값으로 선정되는 경우 알고리즘의 수행 시간이 길어진다

전체 입력 크기의 3/4을 기준으로 good or bad 분할을 구분

* good 분할 확률과 bad 분할 확률은 각각 1/2로 동일하다!

 

선택 문제 알고리즘 시간복잡도

평균 경우 시간 복잡도(= good 분할이 1/2 = 2 * 전부 good 분할인 경우 시간복잡도)

= 2 * O[n + 3/4*n + (3/4)^2*n … (3/4)^i*n] = 2 * O(n) = O(n)

 

이진탐색 알고리즘과 비교

• 범위를 1/2씩 좁혀가는 방식과 피봇으로 분할하는 방식의 차이가 있다
• 부분문제를 취합하는 과정이 별도로 필요 없다는 공통점을 가진다

 

선택 문제 알고리즘 응용

데이터 분석을 위해 중앙값(median)을 찾을 때 활용 (평균값보다 중앙값이 의미 있을 경우 多)

 

최근접 점의 쌍(Closest Pair) 문제

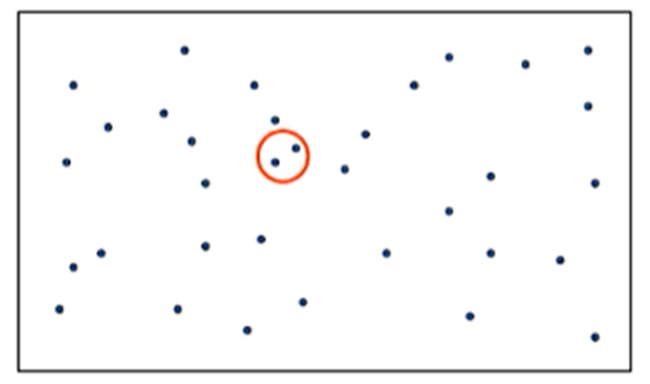
최근접 점의 쌍 문제: 2차원 평면상의 n개의 점이 입력으로 주어질 때, 거리가 가장 가까운 한 쌍의 점을 찾는 문제

 

간단한 방법

• 모든 점에 대하여 각각의 두 점 사이의 거리를 계산해 가장 가까운 점의 쌍을 찾는다
• 전체 점에서 2개 조합의 개수 n(n-1)/2를 모두 계산하는 시간 복잡도 O(n^2)

 

최근접 점의 쌍 분할 정복 알고리즘

해당 문제를 분할한다고 할 때, 경계선에 최근접 점의 쌍이 있을 수 있다

해당 문제를 분할한다고 할 때, 경계선에 최근접 점의 쌍이 있을 수 있다

양쪽 부분해 중에 짧은 값 기준, 중간 영역 안의 점들도 체크해야 한다

x좌표를 기준으로(y 좌표는 생략) 양 쪽 중간 영역의 경계를 체크

양쪽 부분해 중에 짧은 값 (d = min)을 기준으로 중간 영역 범위를 지정

최근접 점의 쌍 분할 정복 알고리즘

최근접 점의 쌍 분할 정복 알고리즘 해설

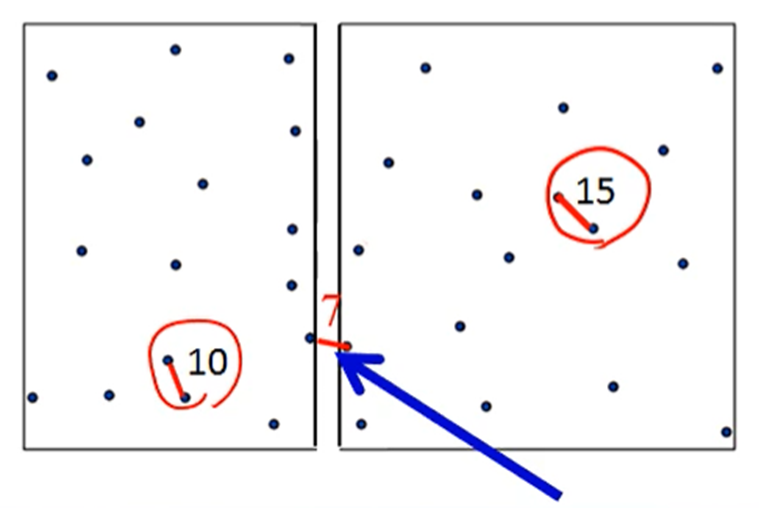
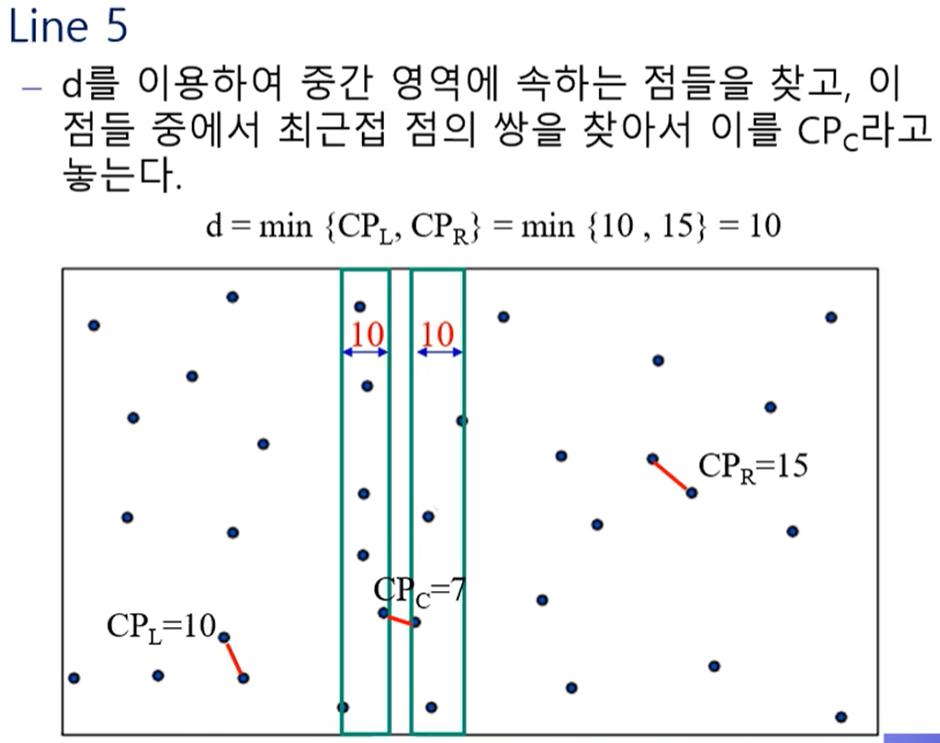
최근접 점의 쌍 분할 정복 알고리즘 과정

 

1. 주어진 배열 S의 크기가 3 보다 크다면 S(L)과 S(R)로 분할

2. S(L)이나 S(R)의 크기가 3이하라면 최근접 쌍의 거리를 반환

3. 각 부분의 최근접 쌍의 거리 중 더 작은 값을 d(=20)라고 할 때, 중간 영역 사이 거리와 비교

4. y좌표로 정렬해 중간 영역 사이 최소 거리 찾기

5. 결론적으로 (CP L) (CP R) (CP C) 중에 가장 짧은 거리를 반환

6. 각 부분해로 상위 중간영역과 다시 비교하여 가장 짧은 거리를 반환

7. 최종 해를 반환

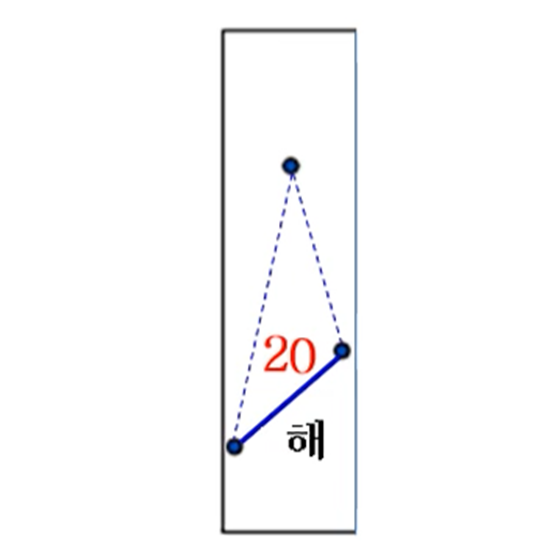
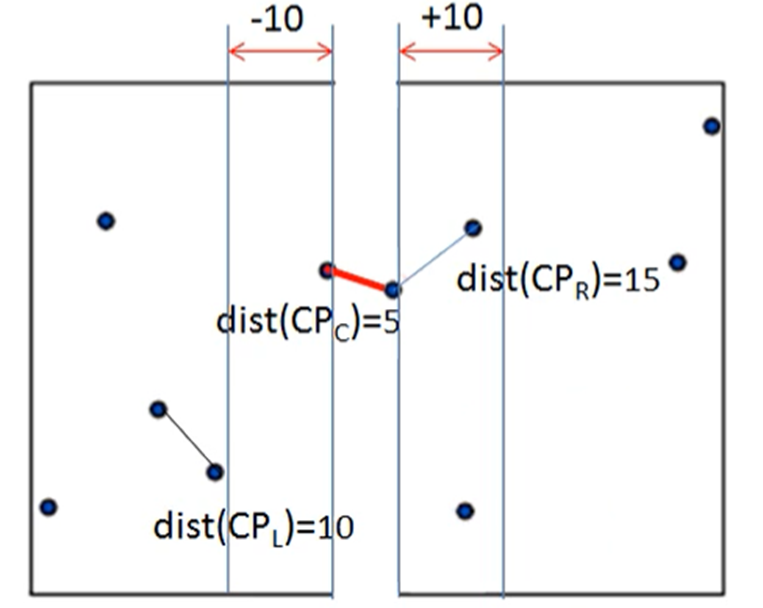
최근접 점의 쌍 분할 정복 알고리즘 시간복잡도

1. 전처리 과정으로 S의 점을 x좌표 기준으로 정렬 ~ O(nlogn)
2. S의 점이 3개라면 3번, 1개라면 1번 거리를 계산 ~ O(1)
3. S를 분할하는 경우 이미 정렬된 배열의 중간 인덱스로 분할 ~ O(1)
4. S(L)과 S(R)에 대해서 재귀 호출하는 과정은 합병 정렬과 동일
5. 중간 영역 최소 거리를 구할 때, y좌표로 정렬 ~ O(nlogn), 주변 점과 비교 ~ O(1)
6. 3개의 점의 쌍 중에 가장 짧은 거리를 가진 값 반환 ~ O(1)
7. 해를 취합하여 올라가는 과정 ~ O(nlogn)
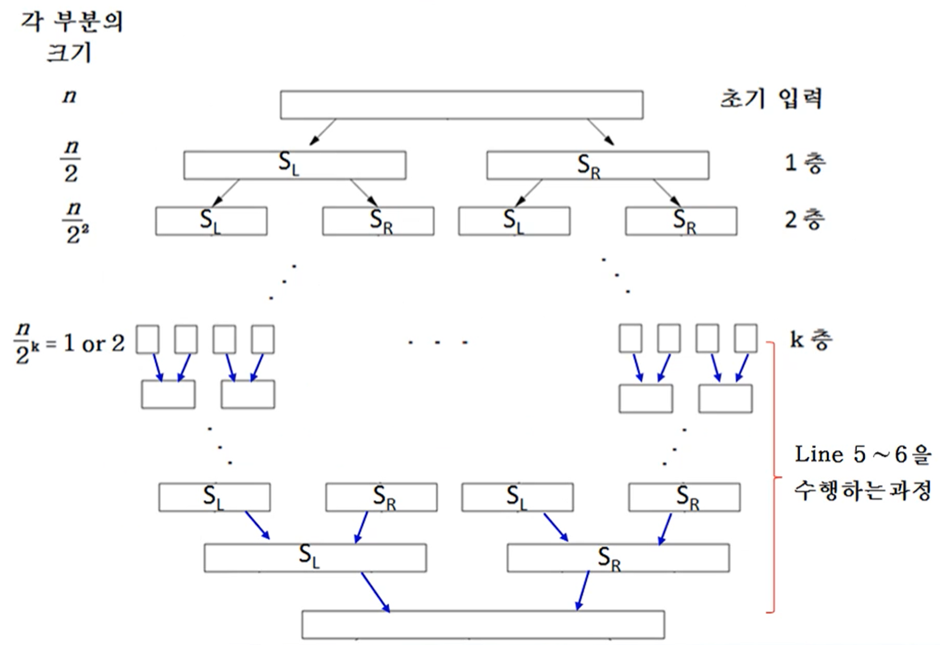
8. k층까지 분할된 후 층 별로 수행되는 과정 = 각 층의 수행 시간 * 층 수 = O(nlogn) * logn = O(nlog^2*n)

최근접 점의 쌍 분할 정복 알고리즘 시간복잡도 정리

최근접 점의 쌍 분할 정복 알고리즘 응용

• 컴퓨터 그래픽스
• 컴퓨터 비전(Vision)
• 지리 정보 시스템(GIS)
• 분자 모델링(Molecular Modeling)
• 항공 트래픽 조정(Air Traffic Control)
• 마케팅(주유소, 프랜차이즈 신규 가맹점 등 위치 선정)