[HUFS/알고리즘] #2 분할 정복 알고리즘(1)

분할 정복 알고리즘(Divide-and-Conquer)

분할 정복: 아우스터리츠 전투에서 유래된 용어로, 대상을 작게 분할해 각각 정복한다는 의미

분할 정복 알고리즘: 알고리즘 문제를 나눌 수 없을 때까지 쪼개고 각각 풂으로써 전체 답을 구하는 방식

 

분할(divide) -> 정복(conquer) -> 결합(combine)

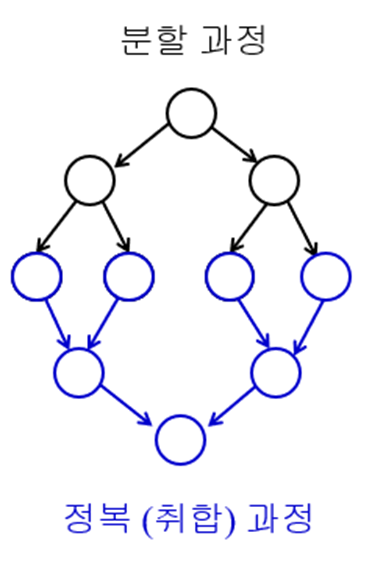
분할된 입력에 대한 문제를 부분문제(subproblem), 부분문제의 해를 부분해라고 한다

부분 문제의 수와 크기에 따라 다음과 같은 분류가 있다

 

문제가 a개로 분할되고, 부분 문제의 크기가 1/b로 감소하는 알고리즘

• a = b = 2인 경우: 합병 정렬, 최근접 점의 쌍 찾기
• a = 3, b = 2인 경우: 큰 정수의 곱셈
• a = 4, b = 2인 경우: 큰 정수의 곱셈
• a = 7, b =2인 경우: 스트라센(Strassen)의 행렬 곱셈

문제가 2개로 분할되고, 부분문제의 크기가 일정하지 않은 크기로 감소하는 알고리즘 

• 퀵 정렬

문제가 2개로 분할되나, 그 중 1개의 부분문제는 고려할 필요가 없으며, 부분문제의 크기가 1/2로 감소하는 알고리즘

• 이진탐색

문제가 2개로 분할되나, 그 중에 1개의 부분문제는 고려할 필요가 없으며, 부분문제의 크기가 일정하지 않은 크기로 감소하는 알고리즘

• 선택 문제 알고리즘

부분문제의 크기가 1, 2개씩 감소하는 알고리즘

• 삽입 정렬, 피보나치 수의 계산

 

합병(=병합) 정렬(Merge Sort)

문제가 2개로 분할되고, 부분 문제의 크기가 1/2로 감소하는 알고리즘

• n개의 숫자들은 n/2개씩 2개의 부분문제로 분할
• 각각의 부분문제를 재귀적으로 합병 정렬
• 2개의 정렬된 부분을 합병하여 정렬(정복)

 

합병 정렬 예시

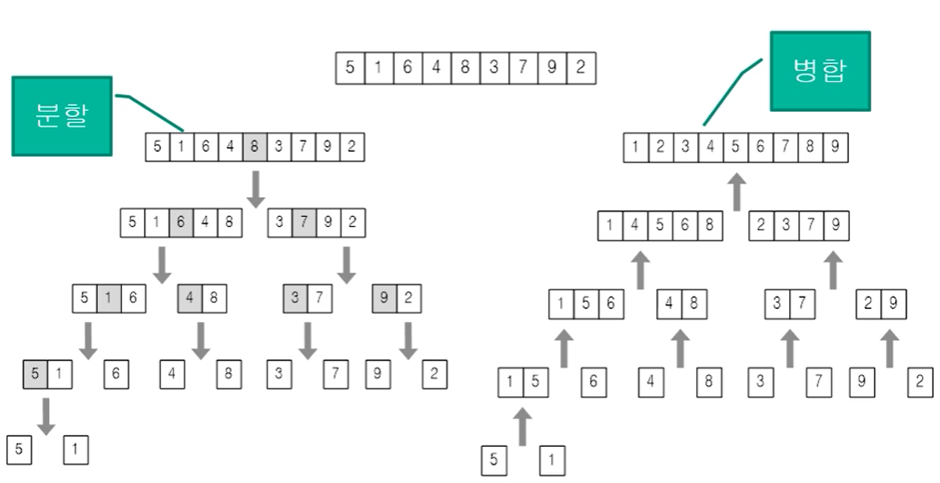
병합 과정에서 정렬하는 법

1. 두 데이터 집합을 합한 만큼 크기의 데이터 집합 준비
2. 두 데이터 집합의 첫 번째 요소들을 비교해 더 작은 요소를 새 데이터 집합에 추가
3. 양쪽 데이터 집합이 빌 때까지 2번 과정을 반복

 

병합 과정에서의 정렬 예시

합병 정렬 알고리즘

합병 정렬 알고리즘 해설

합병 정렬 시간복잡도

 

입력 크기가 8이라면 3개의 층이 만들어진다

입력 크기가 n일 때, k번 분할한다면, 2^k = n이기 때문에 k는 log2(n)

따라서, 시간 복잡도는 (층수) * O(n) = log2(n) * O(n) = O(nlogn)이다

 

합병 정렬 단점

• 대부분 정렬 알고리즘은 입력을 위한 공간 + 변수, 인덱스 등을 담을 공간(O(1))만 사용
• 합병 정렬은 입력과 크기가 같은, 임시 배열을 담을 메모리 공간(O(n))도 별도로 필요

 

합병 정렬 응용

• 합병 정렬은 외부 정렬의 기본이 되는 정렬 알고리즘
• 연결 리스트에 있는 데이터를 정렬할 때, 퀵 정렬이나 힙 정렬보다 효율적
• 멀티코어 CPU나 다수의 프로세서로 구성된 그래픽 처리 장치 등에 활용

 

퀵 정렬(Quick Sort)

피봇(pivot)이라는 배열의 원소를 기준으로 더 작은 값은 왼쪽으로, 더 큰 값은 오른쪽으로 분할하는 방식을 재귀적으로 수행하며 정렬하는 알고리즘

* 분할 후 정복 보다는 정복 후 분할에 가까우며, 분할된 2개의 부분문제의 크기가 일정하지 않다

 

선정된 피봇은 분할에 포함되지 않음

퀵 정렬 알고리즘

퀵 정렬 알고리즘 해설

 

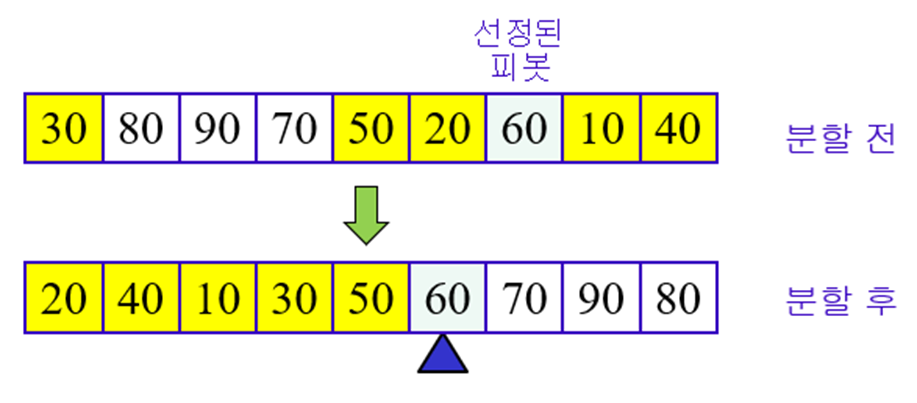
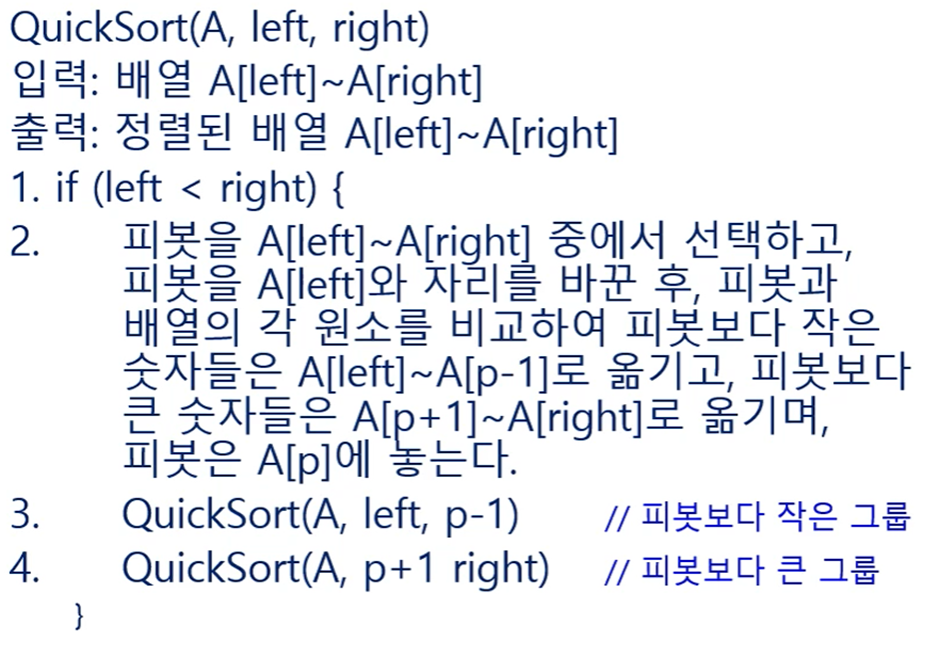
퀵 정렬 알고리즘 수행 과정

 

1. 피봇으로 선정된 값을 가장 왼쪽의 값과 교환

2. 피봇보다 큰 수와 피봇보다 작은 수를 각각 교환

3. 피봇을 피봇보다 작으면서 가장 오른쪽의 값과 교환, 양 쪽으로 분할해 1~3번 반복 (재귀호출)

퀵 정렬 시간 복잡도

• 퀵 정렬의 성능은 피봇 선택에 좌우되는데, 피봇으로 항상 가장 작은 숫자가 선택되거나 항상 가장 큰 숫자가 선택되는 최악의 경우, (n-1) + (n-2) + … + 2 + 1 = n(n-1)/2 = O(n^2)이다
• 거의 반으로 분할되는 최선&평균의 경우, 시간 복잡도는 O(n) * 층수(log2(n)) = O(nlog2(n))이다

 

피봇 선정 방법

1. 완전 랜덤으로 선정하는 경우, 평균적인 시간 복잡도가 나온다
2. 가장 왼쪽, 중간, 오른쪽 숫자 중에서 중앙 값을 피봇으로 정하는 경우

 

이 경우, 26을 피봇으로 선정

퀵 정렬 성능 향상 방법

입력 크기가 매우 커지면, 퀵 정렬과 삽입 정렬을 동시에 사용하면 좋다. 부분 문제의 크기가 일정 기준보다 작아지는 경우, 더 이상의 분할(재귀 호출)을 중단하고 삽입 정렬을 사용하는 것이 더 효율적이다

 

퀵 정렬 응용

• 커다란 입력에 대해 가장 좋은 성능을 보여주는 알고리즘
• 어느 정렬 알고리즘보다 실질적으로 더 좋은 성능을 보임
• 생물 정보 공학에서 특정 유전자를 효율 적으로 찾을 때, 접미 배열과 함께 사용