[HUFS/자료구조] #10 그래프

그래프

그래프란 연결되어 있는 객체 간의 관계를 표현하는 자료구조이다

 

그래프의 예시

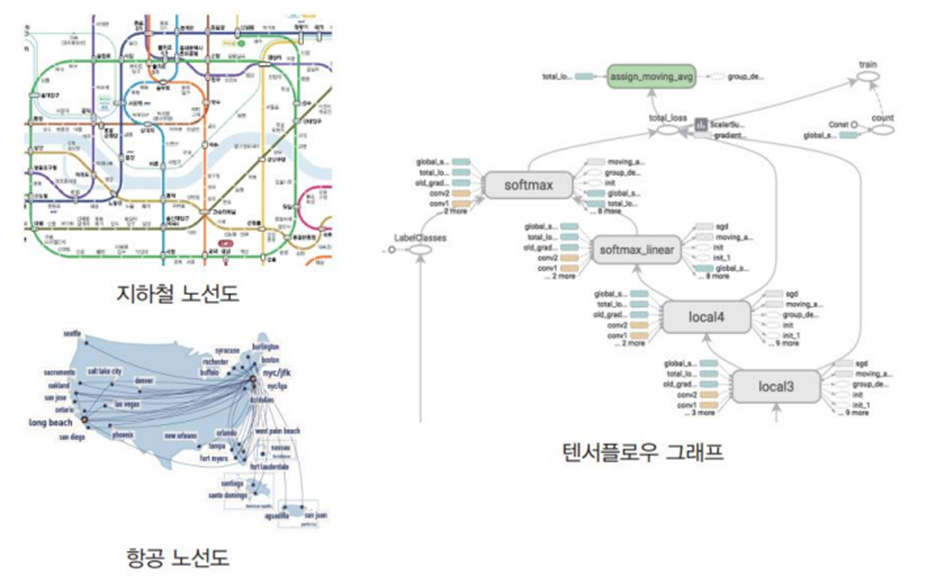
그래프 G는 (V, E)로 표현되며 ‘정점(vertices) or 노드’ / ‘간선(edge) or 링크’ 간의 관계를 의미한다

 

간선의 종류에 따라 무방향 그래프 / 방향 그래프

가중치 그래프, 네트워크 / 부분 그래프

인접 정점과 차수(방향 그래프의 진입/진출 차수)

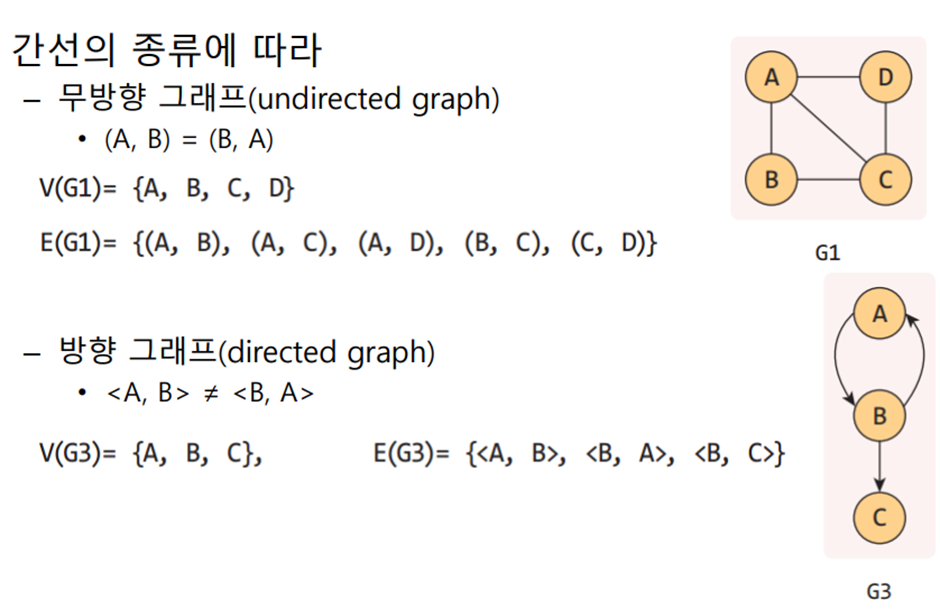
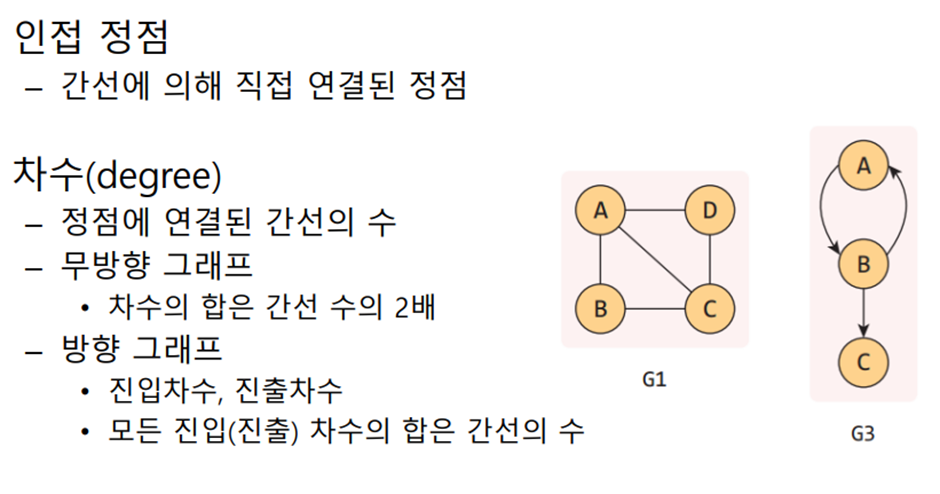
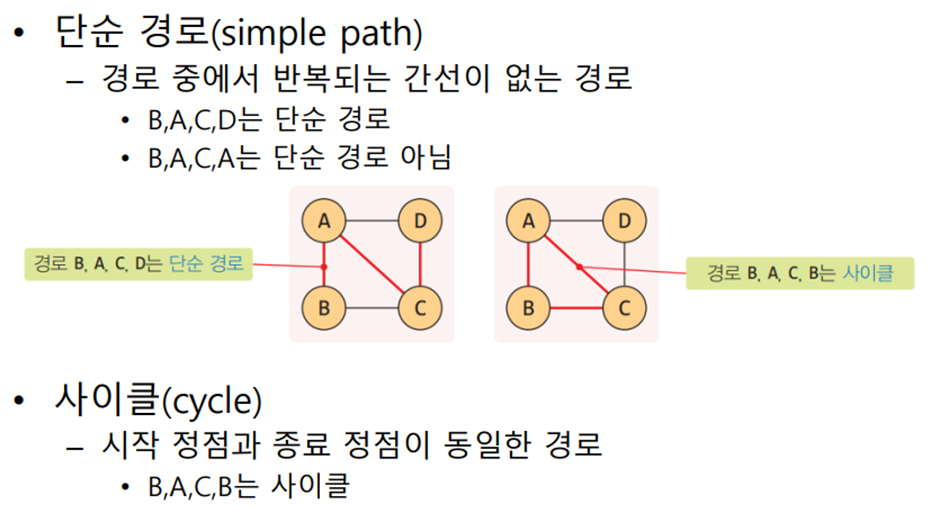
• 그래프의 경로: 정점 간 거쳐가는 경로 ex) B -> A -> C -> D
• 그래프의 길이: 경로 사이의 간선 개수 ex) 3

 

단순경로와 사이클

연결 그래프 / 트리 / 완전 그래프

그래프 ADT(추상자료형)

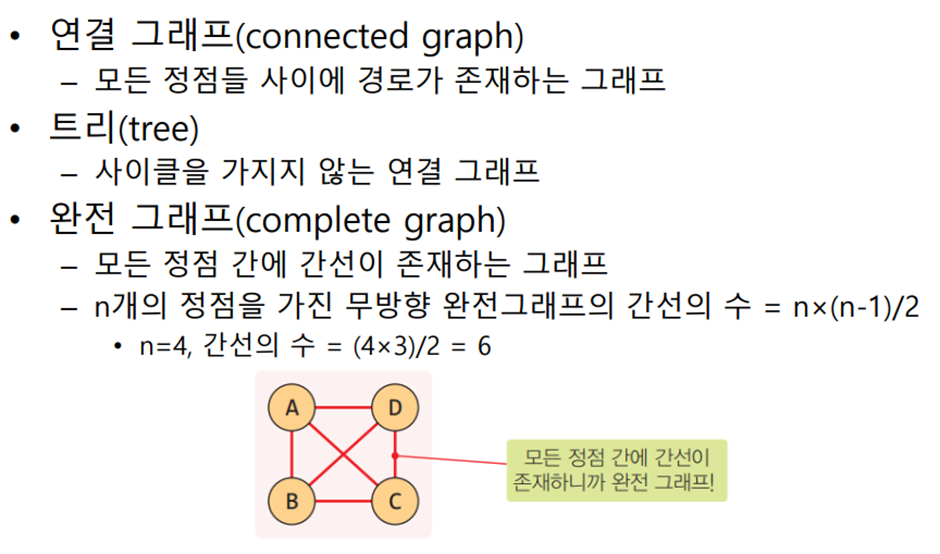
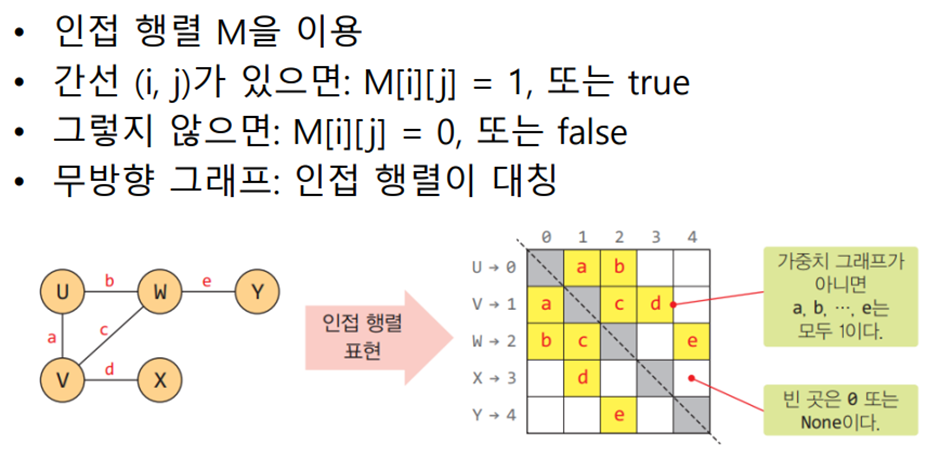
그래프의 표현

그래프를 인접 행렬로 표현 (무방향 그래프인 경우 대칭)

그래프를 인접 리스트로 표현 (단순히 연결된 정점만 표현)

인접 행렬과 인접 리스트의 시간 복잡도 비교

파이썬으로 인접 행렬 표현

파이썬으로 인접 리스트 표현: 인덱스의 리스트

파이썬으로 인접 리스트 표현: 딕셔너리와 인접 정점 집합

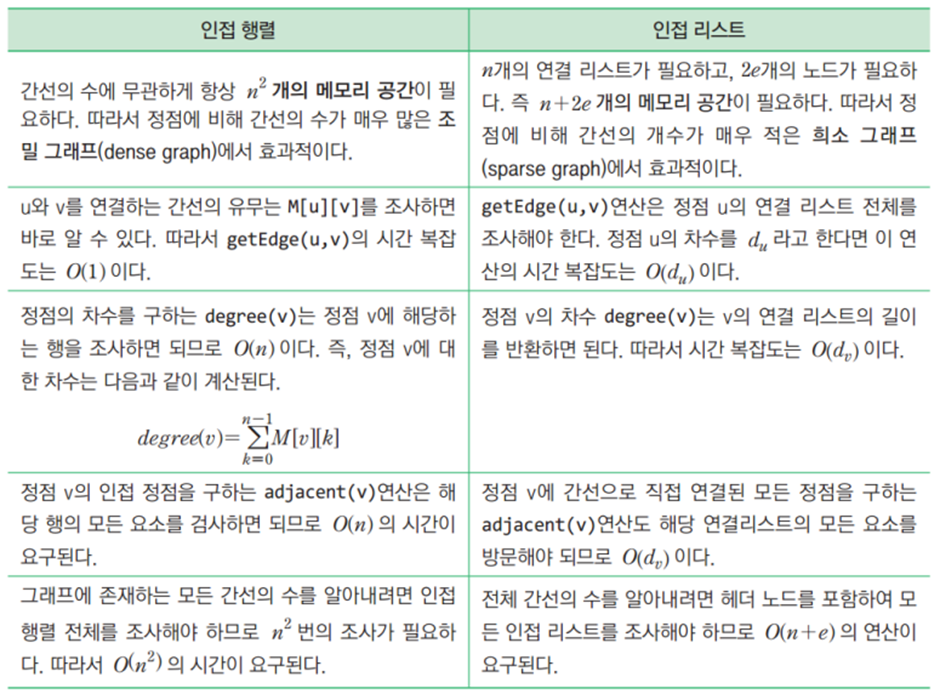
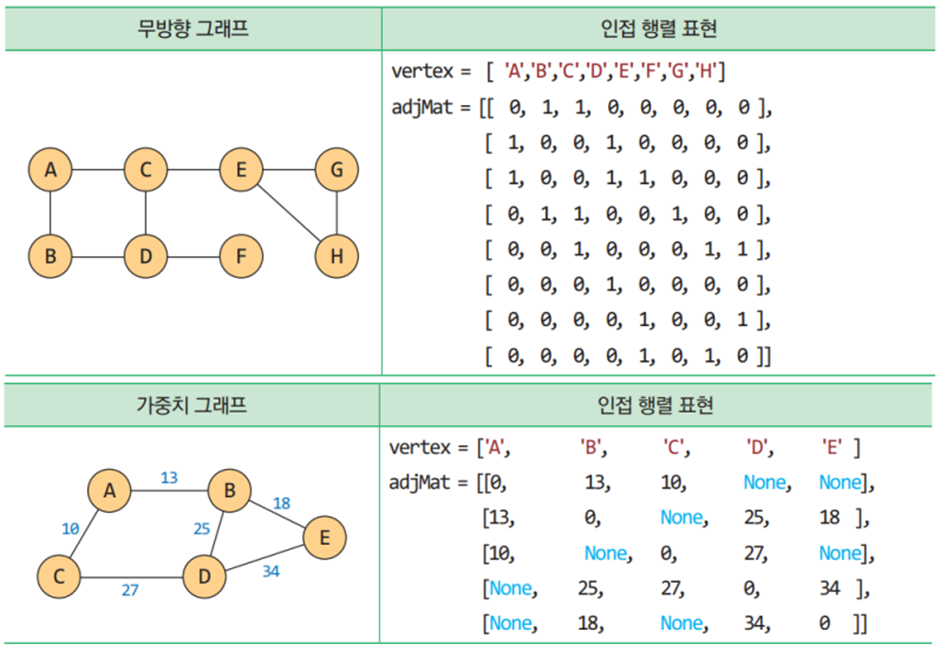
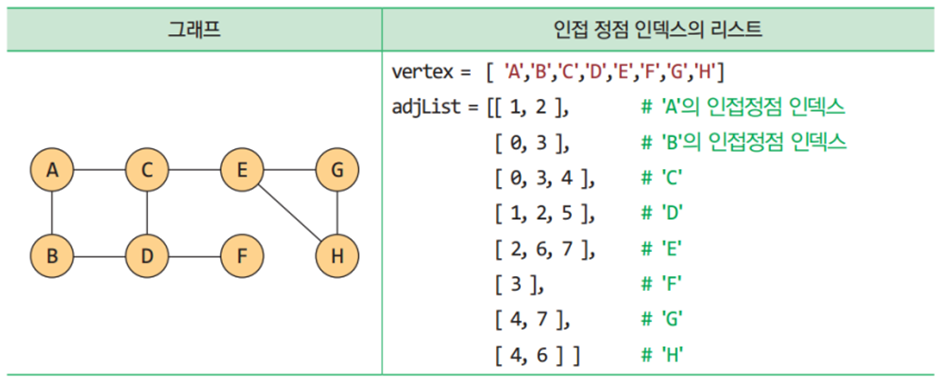
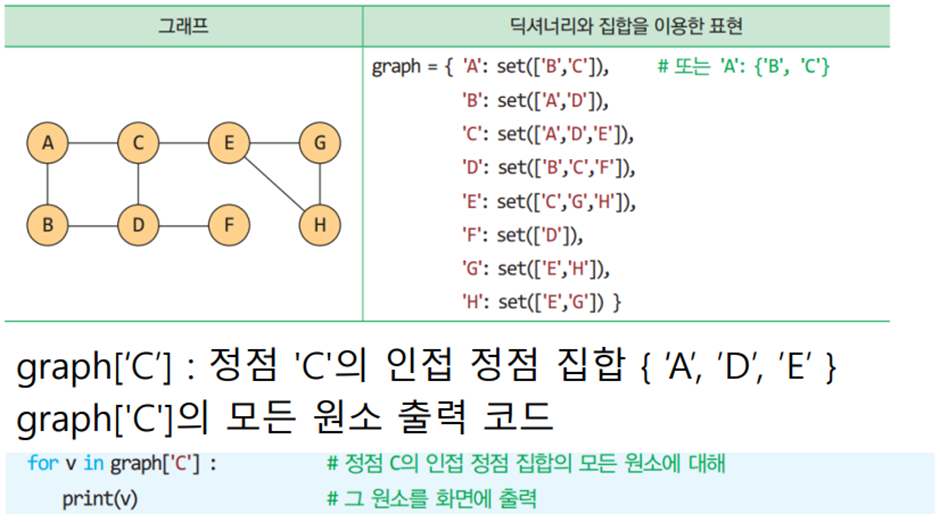
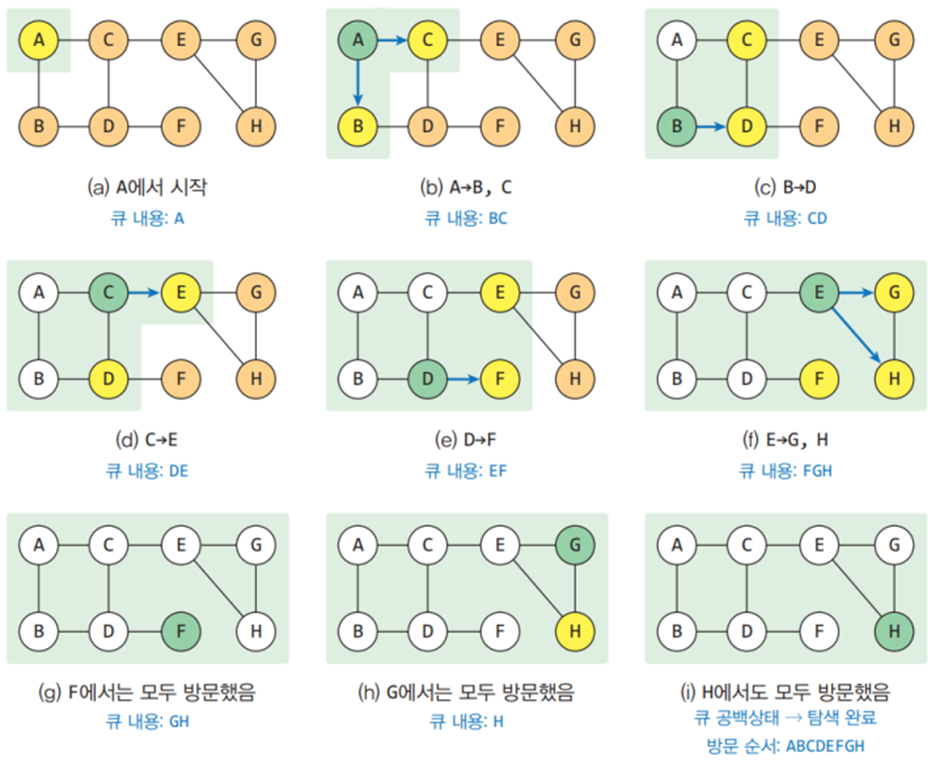
그래프의 탐색

그래프의 탐색은 시작 정점부터 차례대로 모든 정점들을 한 번씩 방문하는 방법으로,

깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS)이 있다

 

도로망이나 전자회로 등 많은 문제들에 탐색이 사용된다

깊이 우선 탐색 알고리즘

깊이 우선 탐색 과정

너비 우선 탐색 알고리즘

너비 우선 탐색 과정

탐색 알고리즘 성능

최대로 연결된 그래프들을 보며 연결 성분을 검사한다

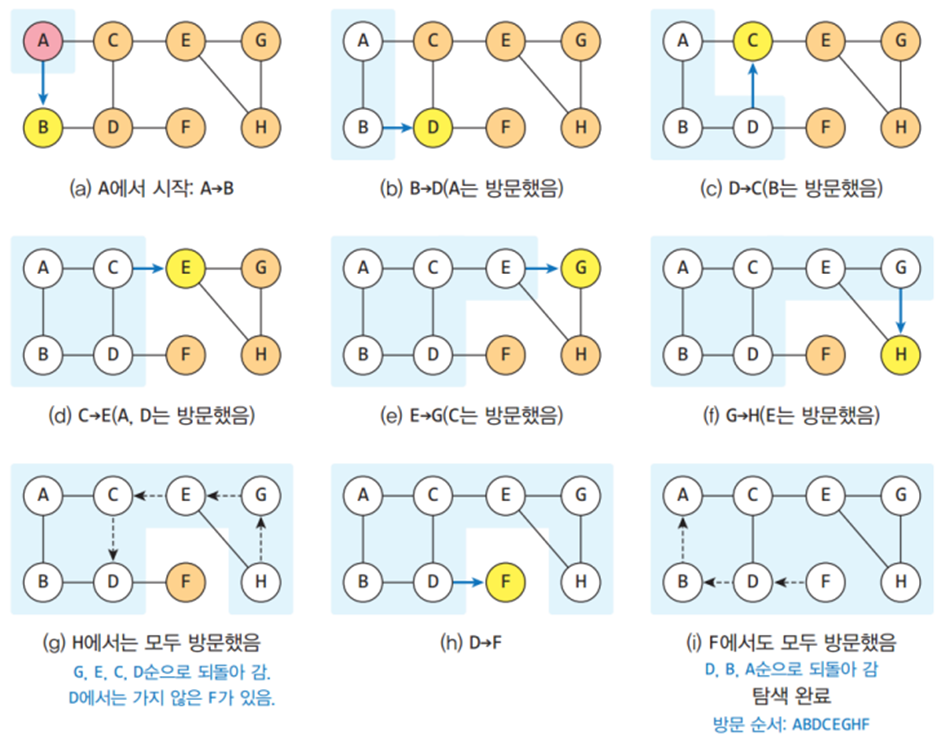
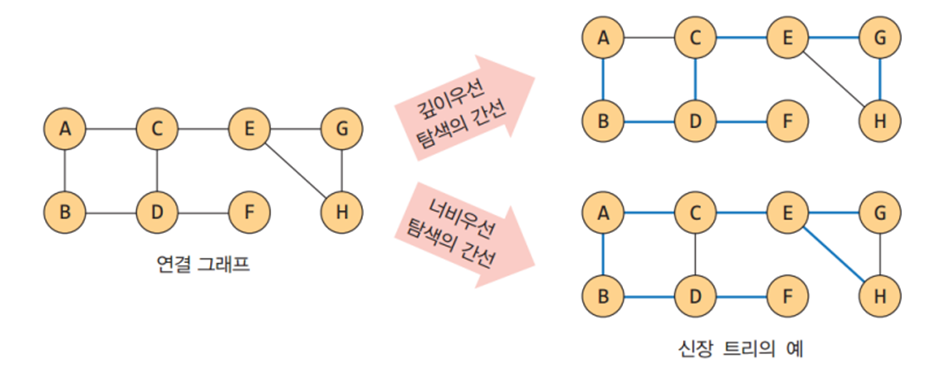
신장 트리

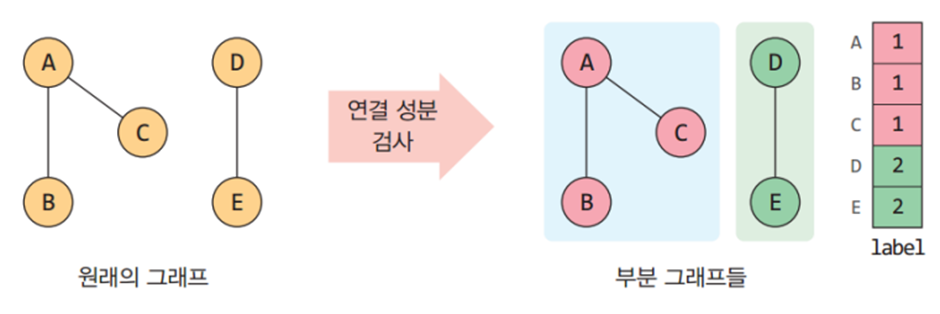
신장 트리란 그래프 내의 모든 정점을 포함하는 트리로 사이클을 포함하면 안된다

 

간선의 수 = n-1

신장 트리 알고리즘

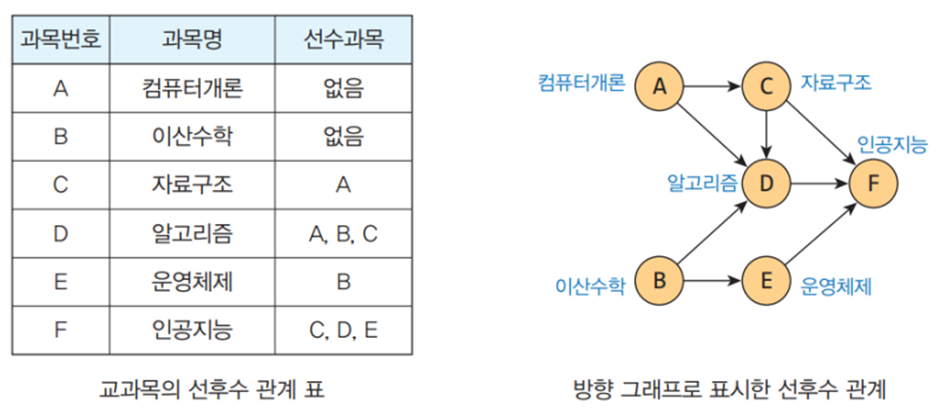
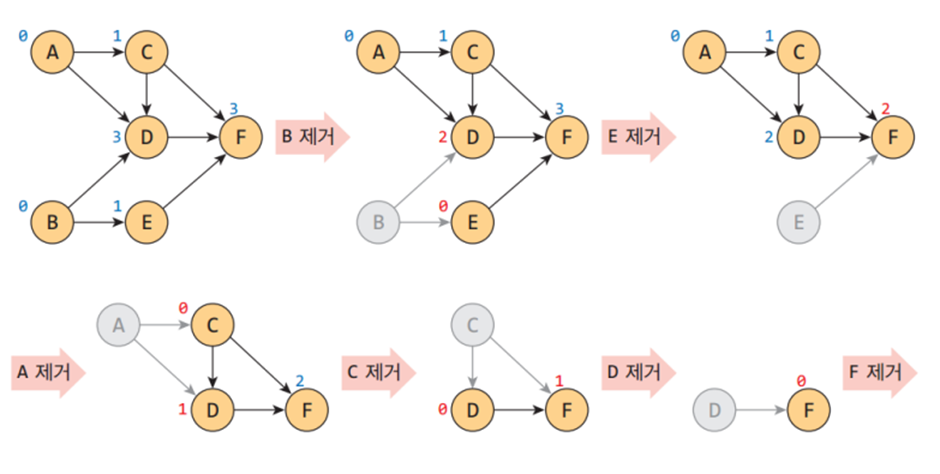
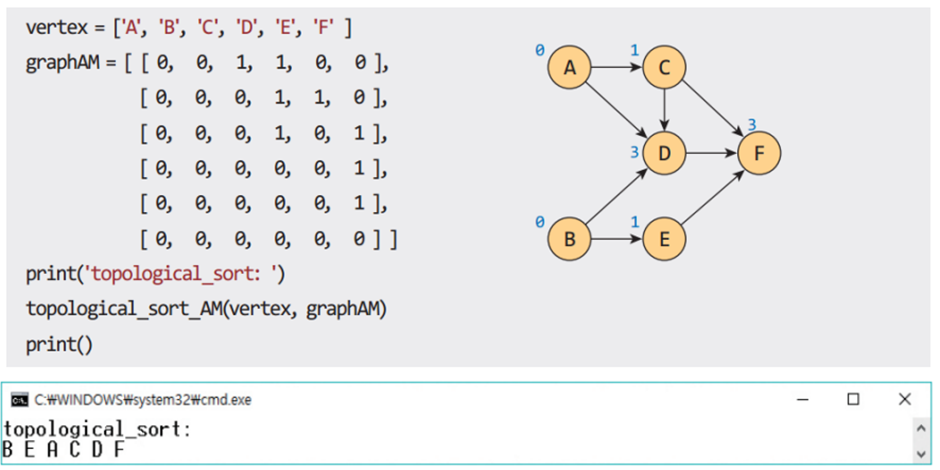
위상 정렬

위상 정렬이란 방향 그래프에 대해 정점들의 선행 순서를 위반하지 않으면서 모든 정점을 나열하는 것

 

선수 관계에 따른 진입/진출 간선

위상 정렬 과정 (제거에 따른 진입 차수 변화) B-E-A-C-D-F

위상 정렬 알고리즘

위상 정렬 테스트 프로그램

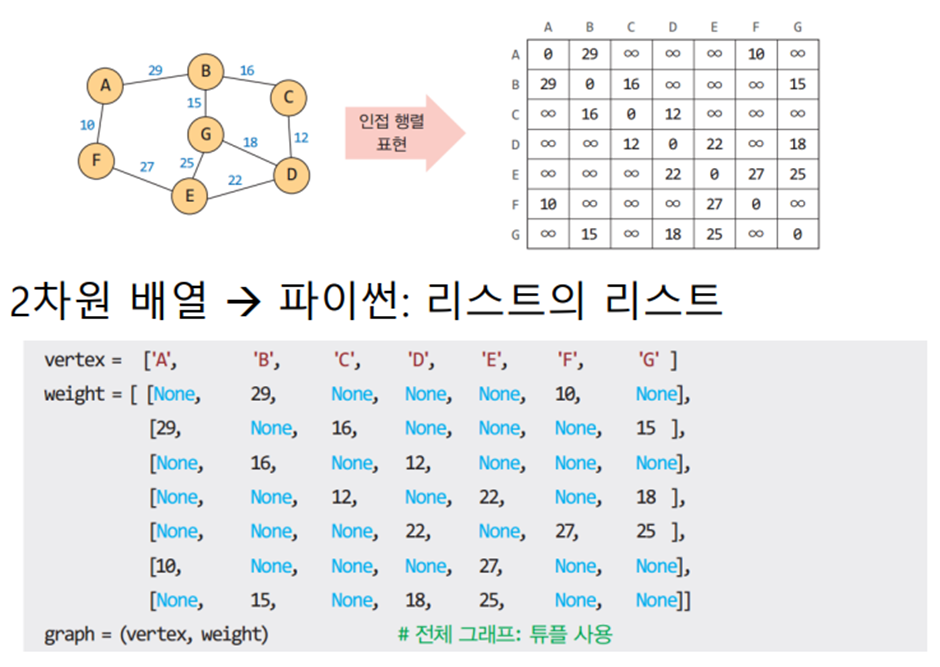
가중치 그래프

간선에 가중치가 할당된 그래프이며 G = (V, E, w)로 표현한다 (w: 비용/가중치/길이)

 

인접 행렬로 가중치 그래프 표현

인접 행렬에서의 가중치 합 연산

인접 행렬에서의 모든 간선 출력

인접 리스트로 가중치 그래프 표현

인접 리스트에서의 가중치 합 계산

인접 리스트에서의 모든 간선 출력 / 테스트 프로그램

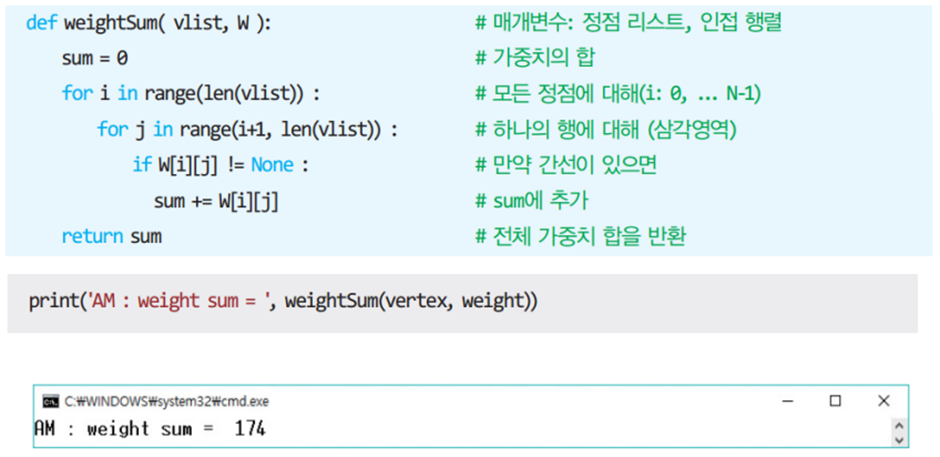
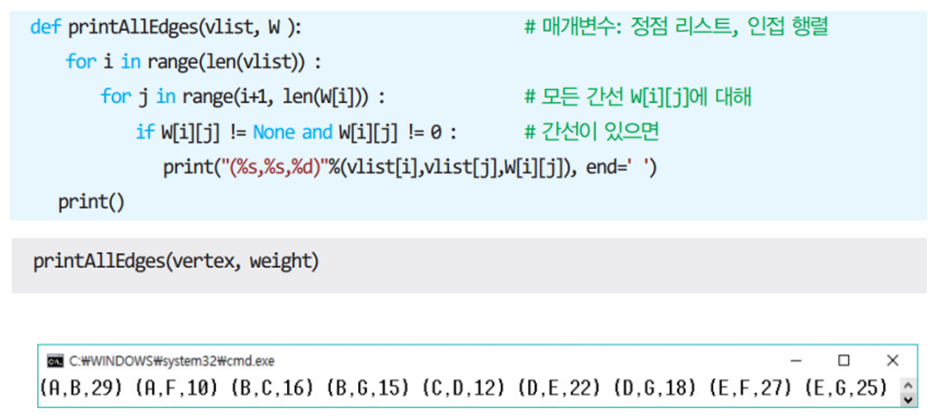
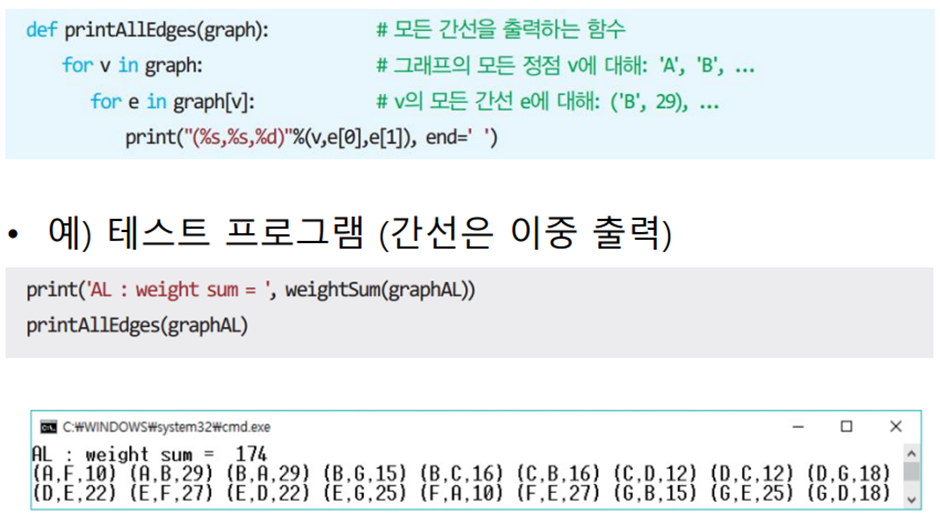
최소비용 신장 트리

간선들의 가중치 합이 최소인 신장 트리 ~ (n-1)개의 간선만 사용하며 사이클 미포함

* 도로, 통신, 배관, 전기 회로 등 길이/비용을 최소화하는 분야에 응용된다

 

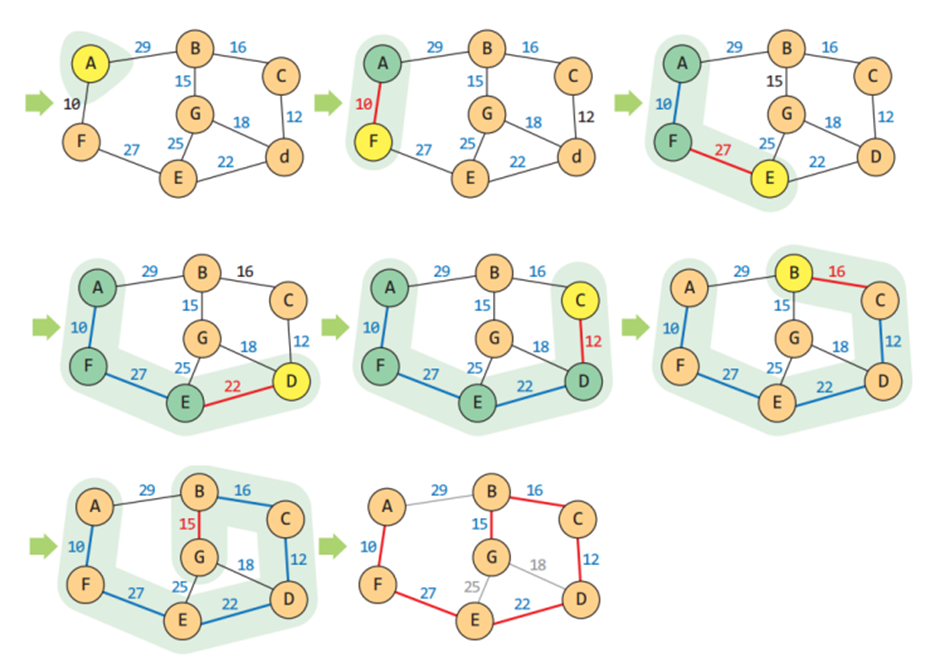
Kruskal의 MST 알고리즘은 각 단계에서 최선의 답을 선택해 최종적 해답에 도달하는 탐욕적 방법(greedy method)을 따른다

 

Kruskal의 최소 비용 신장 트리 알고리즘 조건

Kruskal의 MST 과정 (간선의 수와 사이클을 고려해 최소비용 간선 선택)

union-find 알고리즘의 집합을 통해 사이클 여부를 검사할 수 있다

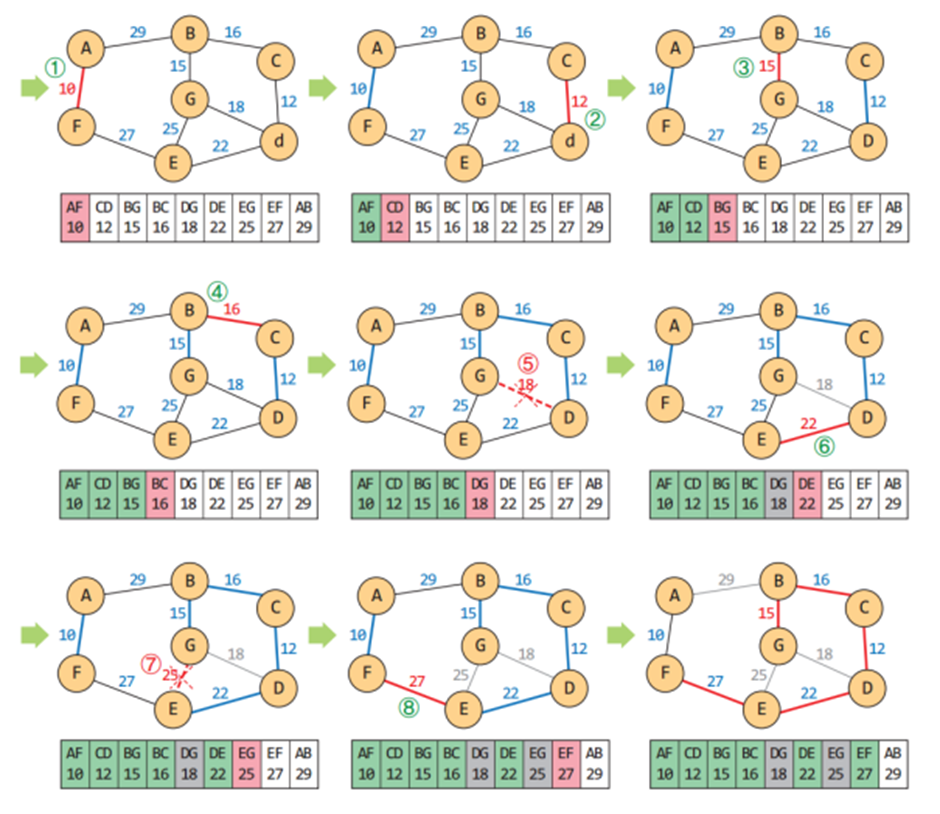
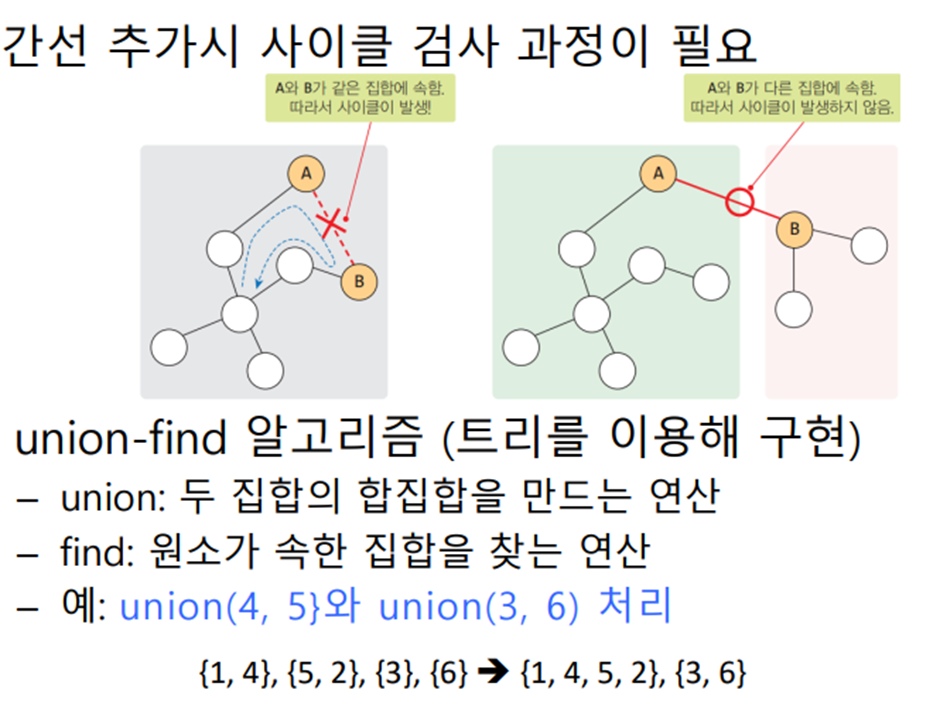
Prim의 MST 알고리즘은 하나의 정점에서부터 트리를 단계적으로 확장한다

 

Prim의 최소 비용 신장 트리 알고리즘 조건 (n-1개의 간선을 가질 때까지 반복)

Prim의 MST 과정

MST 알고리즘 시간 복잡도 (Prim이 실생활에는 더 많이 사용)

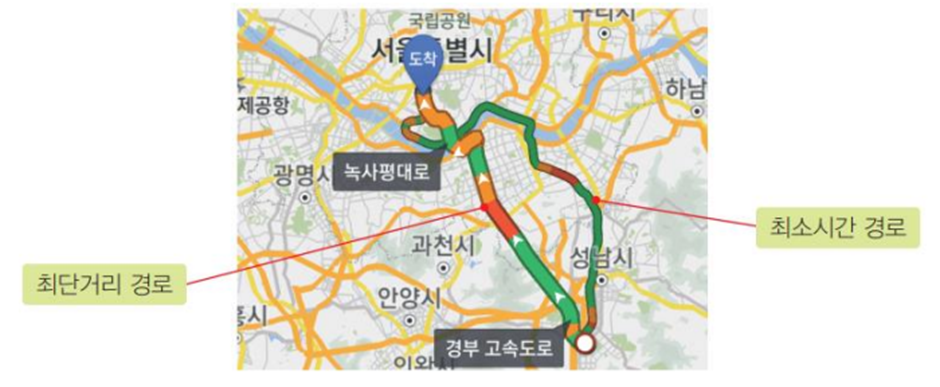
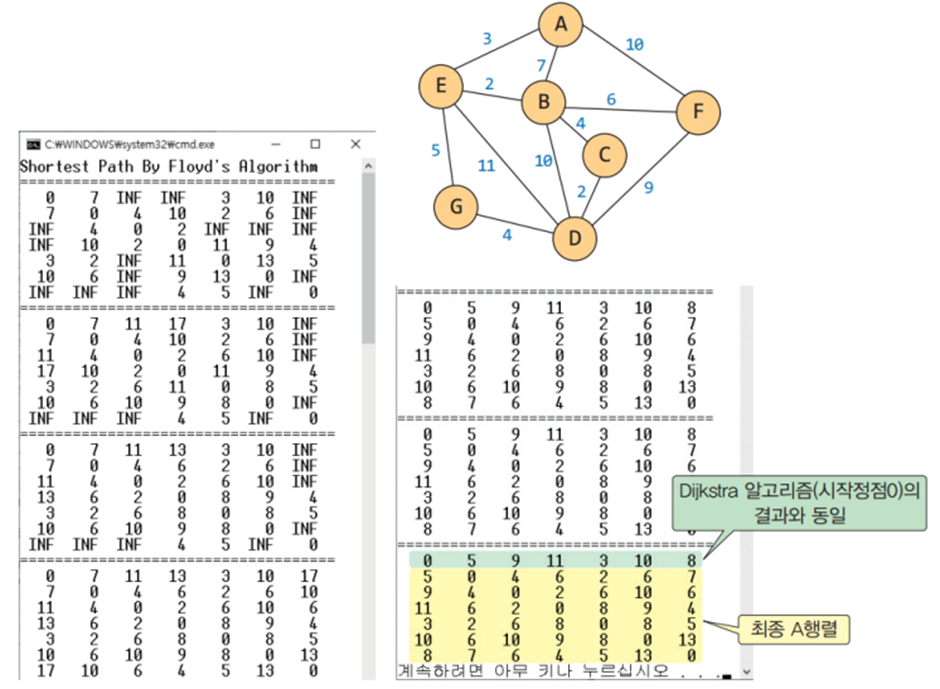
최단 경로

최단 경로 알고리즘이란 정점 u와 정점 v를 연결하는 경로들 중 간선들의 가중치 합이 최소가 되는 경로

 

최단 거리 / 최소 시간의 차이

인접 행렬로 최단 경로 그래프 표현

다익스트라(Dijkstra) 최단 경로 알고리즘

최단 경로 증명

새로운 정점이 S에 추가되면 dist 갱신 (뭐가 더 짧은지 함수로 갱신)

다익스트라(Dijkstra) 알고리즘

테스트 프로그램

알고리즘 실행 과정1

알고리즘 실행 과정2

모든 정점 사이의 최단 경로

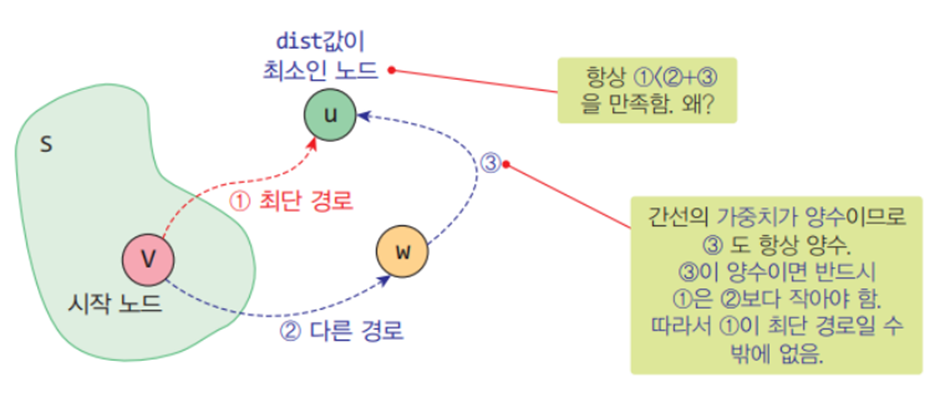
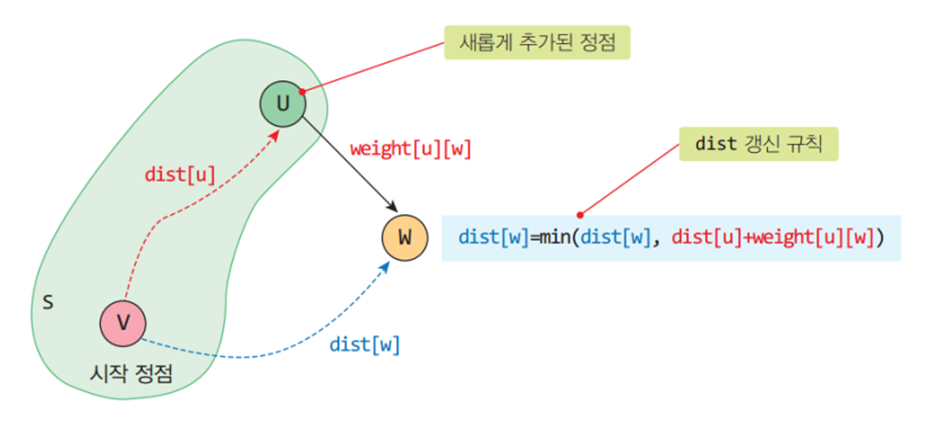
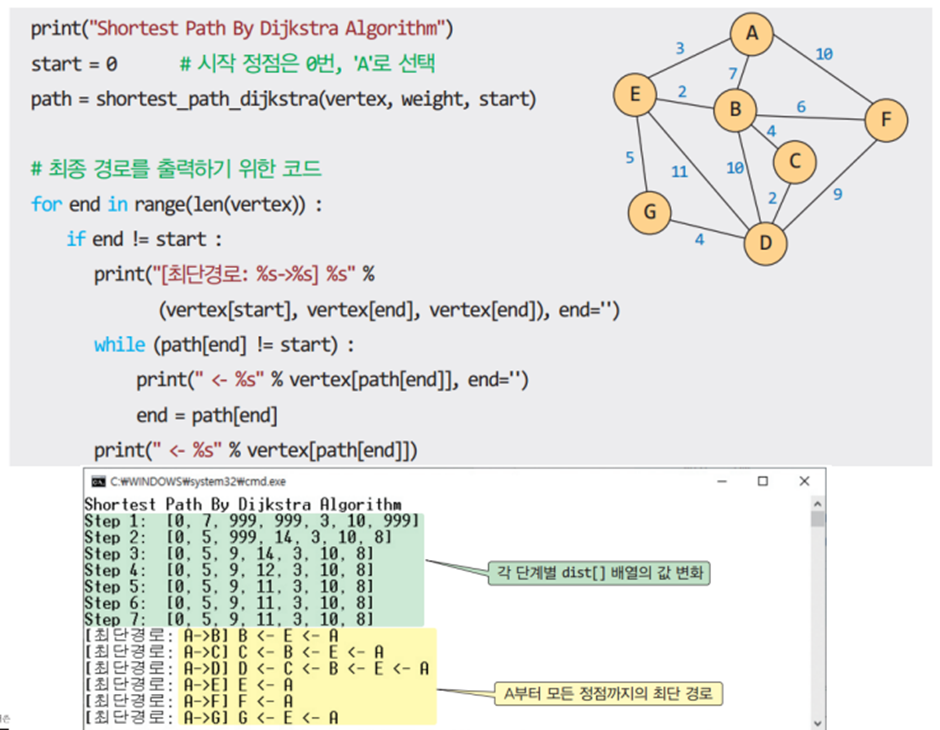
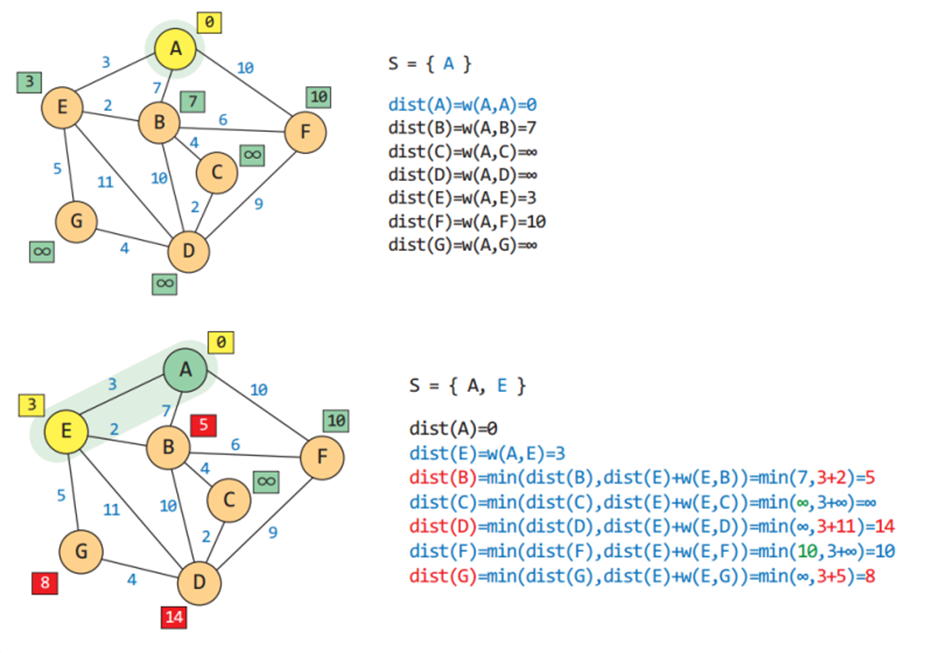
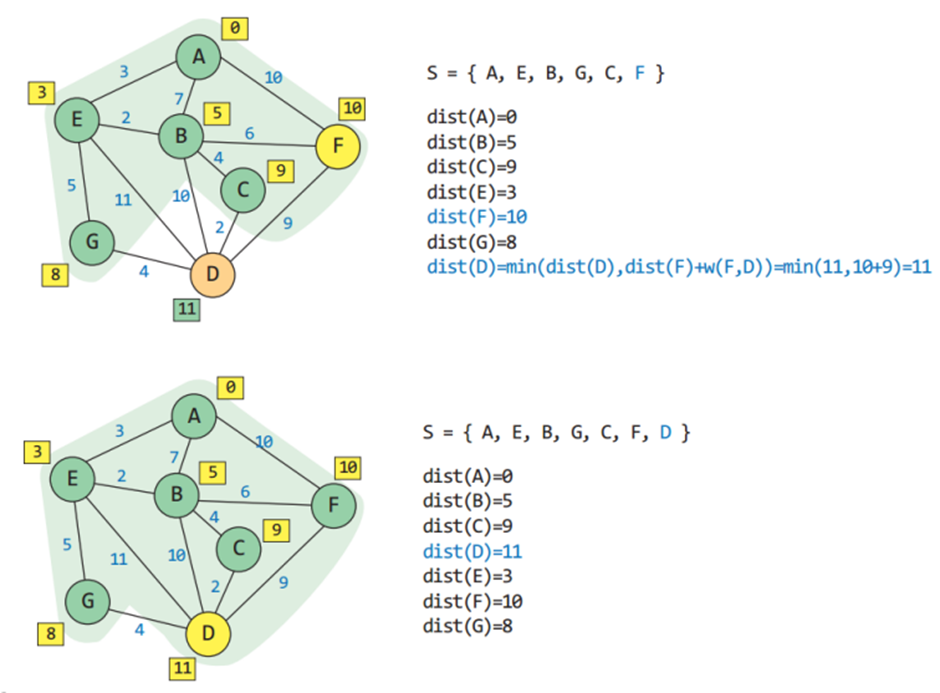
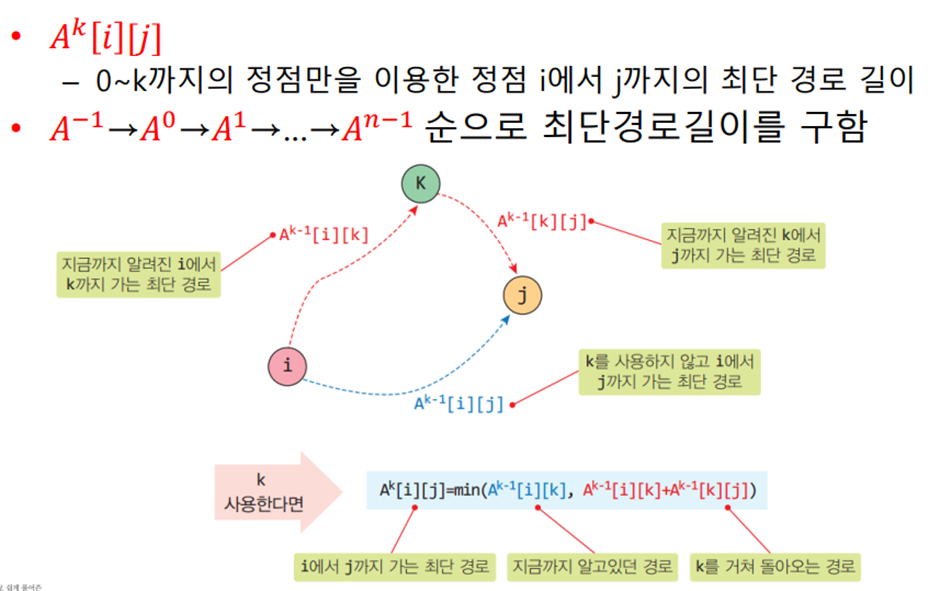
* 2차원 배열 A를 이용하여 3중 반복하는 루프로 구성되며 초기 값은 인접 행렬의 가중치이다

 

Floyd 알고리즘 아이디어

Floyd 알고리즘

실행 결과

Dikstra/Floyd 최단 경로 알고리즘 시간 복잡도 비교