[HUFS/데이터베이스] #12 데이터 종속성과 정규화

데이터의 논리적 표현

스키마 설계 = 데이터베이스의 논리적 설계

1. 애트리뷰트, 엔티티, 관계성 파악
2. 관련된 애트리뷰트들을 릴레이션으로 묶기 (데이터 종속성 고려: 학번 ~ 학생)
3. 데이터 변경(삽입, 삭제, 변경) 시 이상현상 대비

이상(anomaly)현상이란?

• 삭제 이상: 연쇄 삭제에 의한 정보 손실
• 삽입 이상: 원하지 않는 정보의 강제 삽입
• 갱신 이상: 중복 데이터의 일부 갱신으로 정보의 모순성 발생

 

해결책: 애트리뷰트들 간의 여러 종속관계를 분해하여 각각의 릴레이션으로 표현

하나의 종속성을 하나의 릴레이션으로 -> 정규화 과정

 

정규형(normal form): 이상 현상이 발생하지 않도록 제약 조건을 만족하는 릴레이션

스키마 변환: 애트리뷰트들과 제약조건(종속성)을 수집한 후 여러 릴레이션으로 분할

외부 스키마 -> 논리 스키마 -> 내부 스키마

‘정보 표현의 무손실 / 최소의 데이터 중복 / 분리의 원칙’을 따라야 함

 

함수 종속

릴레이션 R에서 애트리뷰트 X의 값 각각에 대해 애트리뷰트 Y의 값이 최대 하나만 연관

= 애트리뷰트 Y가 애트리뷰트 X에 함수 종속된 관계 (X(학번) -> Y(학생이름))

* X나 Y는 각각 두 개 이상의 집합이 될 수 있다

ex) X(학번) -> Y(학생이름, 학년, 학과) / X(학번, 과목번호) -> Y(학점)

 

릴레이션 R에서 애트리뷰트 X가 키라면 ‘R의 모든 Y에 대해서 X -> Y 성립’

* 실제 이러 종속관계들을 도메인(특정 분야) 전문가와 데이터베이스 전문가가 협의해 도출함

 

함수 종속 관계들을 함수 종속 다이어그램으로 나타낼 수 있다

 

2 개 이상으로 구성된 집합  X 에 대해서  X->Y 가 성립할 때

• 완전 함수 종속: X의 부분집합 중 X->Y가 성립되는 경우가 없는 경우
• 부분 함수 종속: X의 부분집합 중 X->Y가 성립되는 경우가 있는 경우

 

ex) X(학번, 과목번호) -> Y(성적) = 완전 함수 종속 / X(학번) -> Y(학년)

 

함수 종속에 대해 성립하는 추론 규칙들

 

함수 종속을 통해 또다른 함수 종속을 유도해 찾아냄

제1정규형(1NF)

모든 도메인이 원자 값으로만 이루어진 릴레이션

 

1NF 예시

1NF에서는 다음과 같은 이상 현상이 발생할 수 있다

1. 삽입이상: 기본키를 모두 충족하지 않는 삽입을 시도할 경우 ex) 과목번호 없이 학번만 삽입
2. 삭제이상: 종속 관계에 있는 정보 연쇄 삭제로 정보 손실
3. 갱신이상: 기본키가 같은 모든 튜플을 한 번에 변경하지 않는 경우

1NF 이상의 해결 -> 프로젝션으로 부분 함수 종속을 제거 = 2NF

 

제2정규형(2NF)

1NF 중에서 키에 속하지 않는 애트리뷰트들이 모두 기본 키에 완전 함수 종속된 상태

 

1NF를 2개 이상의 릴레이션으로 무손실 분해 후 프로젝션

무손실 분해: 자연 조인을 통해 원래의 릴레이션으로 복귀 가능한 분해

ex) R(A,B,C)에서 A->B가 성립하면 R1(A,B) R2(A,C)로 정보 손실 없이 분해

 

2NF 예시 (학번이 외래 키) ~ 부분 함수 종속 제거/1NF에서의 이상 해결

이행적 함수 종속이 발생하기 때문에 여전히 삽입/삭제/갱신 이상인 경우 존재

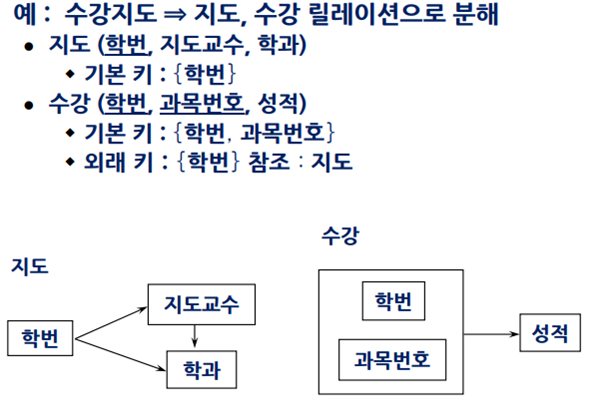
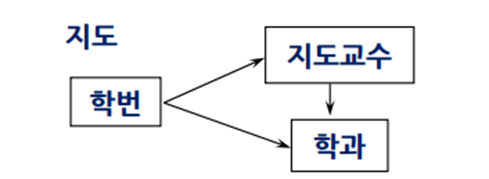
A -> B -> C 형태의 이행적 함수 종속을 3NF로 분해해서 이상 해결

 

제3정규형(3NF)

2NF이면서 키가 아닌 모든 애트리뷰트들은 기본 키에 이행적 함수 종속이 되지 않는 상태

 

마찬가지로 한 번 더 무손실 분해

한 쪽은 키, 한 쪽은 외래 키가 되며 제2정규형 이상들을 해결

모든 이원 릴레이션은 3NF에 속하며 다음과 같은 경우에는 3NF 적용 불가

~ 복수의 후보 키를 가지거나 후보 키들이 두 개 이상의 애트리뷰트들로 구성되거나 중첩될 때

다만 3NF역시 결정자가 후보 키가 아닌 경우에는 이상 발생!

 

릴레이션 R의 결정자가 모두 후보 키인 경우 보이스/코드 정규형(BCNF)이라고 한다

 

BCNF를 따른다면 자동적으로 1/2/3NF에도 속한다

BCNF를 따르는 반복적인 그룹이 있을 때 중복 행이 있어도 갱신 이상 발생 가능

 

제4정규형(4NF)

이처럼 값 하나가 아닌 값의 집합을 결정하는 다치 종속(MVD)의 경우,

각각 독립된 정규형으로 분해해야 하는데 이를 제4정규형(4NF)이라고 한다

 

제4정규형으로 분해

릴레이션 R에서 다치 종속 A->B를 만족하는 애트리뷰트 집합 A, B가 존재할 때,

R의 모든 애트리뷰트들이 A에 함수 종속이면 R은 제4정규형(4NF)이다

(= BCNF에 속하는 릴레이션 R의 모든 MVD가 FD인 경우)

 

제5정규형(5NF)

SCP(SN,CN,PN) 릴레이션: 공급자(SN)가 부품(CN)을 프로젝트(PN)에 제공함을 표현

SCP 릴레이션은 4NF이며 모든 애트리뷰트가 키에 속하고 FD나 MVD 존재X

 

3개의 릴레이션을 무손실 분해되는데 2번 조인해야 재생성 가능

즉 3개를 전부 조인해야 재생성이 되는 3-way 순환 제약조건을 따른다

이런 식으로 n-way cycle constraint를 만족하면 n-분해 릴레이션이며,

이는 n개의 프로젝션으로만 무손실 분해 될 수 있으며 그 이하로는 분해가 불가능하다!

즉, n개로 분해할 때만 조인 종속(JD: Join Dependency)을 만족하는 것

모든 조인 종속에 따라 분해하는 제5정규형은 프로젝션-조인 정규형이라고도 하며 매우 드문 경우이다

 

정규형 과정 및 종속 간의 포함 관계를 정리하면 이와 같다

이처럼 이상 현상이 생기지 않도록 릴레이션을 분해하며 좋은 스키마를 설계해야 한다!

~ DB는 스키마를 무손실 분해/조인하면서 사용자의 질의를 처리한다